３１．シミュレーション

本日の授業では、シミュレーションプログラムの実装について学びます。高校1年生の情報Ⅰの授業で、私たちが自分の手でプログラムを組んで理解を深めることに挑戦します。特に斜方投射という物理現象を、コードに落とし込みます。

黒板

授業

シミュレーションとは

シミュレーションとはコンピュータを利用し、現象や動作を模擬実験により再現することをいうよ。コストや時間がかかるもの、一度しかできないもの、危険をともなうものなどをモデル化し、問題解決を図るためにシミュレーションが利用されるんだ。

気候変動をコンピュータでシミュレーションしている様子はニュースで見たな。あれは、ノーベル賞を受賞した真鍋先生が作ったモデルを使っているって報じていたよ、

おっ。ニュースをよく見ているね。真鍋先生のモデルは、気候の過去・現在・未来をシミュレートできるんだ。だけど100%正確な予測は難しいよ。

へぇー。モデルを作って、コンピューターにお任せってできるわけではないんだね。

そうなんだ。新しいデータが得られるたびに、モデルを見直したり、複数のモデルの予測結果を統合することで、精度を上げるといった取り組みをしているんだ。

ノーベル賞を取るには、努力が欠かせないということですね。日々精進します・・・

いいね。いきなりノーベル賞レベルは難しいから、もう少し身近なテーマでシミュレーションプログラムを作ってみよう。飛んでいるボールがどこあたりに落ちるか？というシミュレーションをやってみるけどいいかな？

おっ！このシミュレーションができれば、外野フライを取り損なうことがなくなるかも!

よろしくお願いします。

斜方投射の論理モデル

今回モデルを実装するのは。「斜方投射」のモデルだ。斜方投射というのは、物体を斜めに投げたときの運動のことを指すんだ。実際にボールを投げて、その動きを計算する実験から、ボールの動きには法則があることがわかっているんだ。それを論理モデルにすると以下の通り。

実際には、風やボールの回転などの影響もありますよね。それが読めないから、いつもフライを取り損なうんだけど。

鋭いね。要素をふやすと、複雑になってしまうので、今回は外部環境の変化は無視したものとするよ。

なるほど。モデル化のところで習った「次元の呪い」ですね。

斜方投射のアルゴリズム

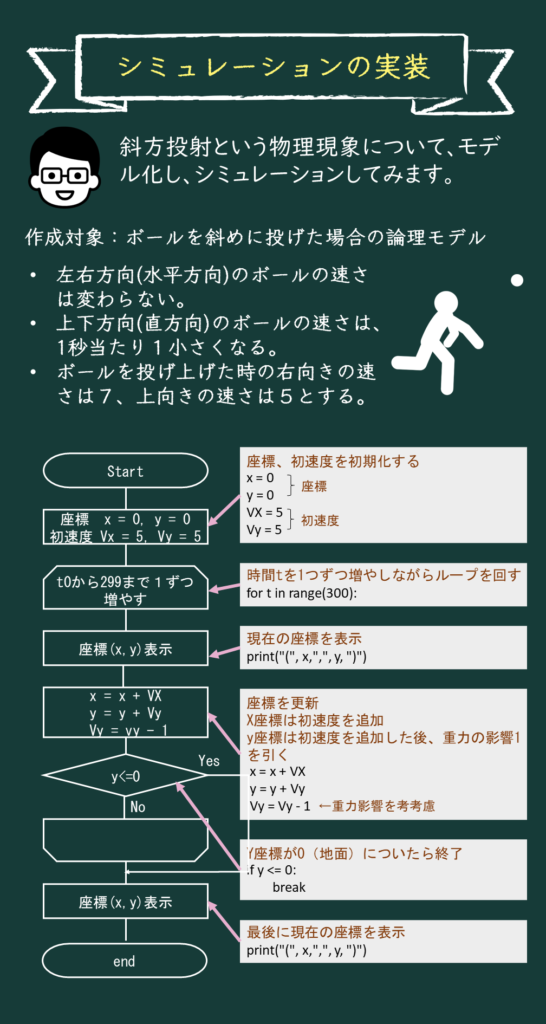
まずはアルゴリズムを考えよう。まずボールの位置を表す変数x、yを用意する。初期値は0だ。

ふむふむ。x座標と、y座標ですね

次に速度を表す変数Vx、Vyを用意する。今回は右向きの速度を5、上向きの速度を5としよう。この値は条件によって変えていいよ。

上方向と横方向の速度が同じという事は、ちょうど斜め45度の角度で投げたってことですね？

その通り。そして時間tをループ変数として、ループをを回すんだ。ここではtの最大値は仮に300でタイムアウトするようにしておくよ。

なんでタイムアウトを設けているの？

このシミュレーションは、ボールが落ちてきたら終わりなんだけれど、プログラムやデータにミスがあった場合、いつまでも落ちてこない。

そうなると、無限ルームになって、暴走しちゃいますね。無限ループにならないようにプログラムを作ることは重要ですね。

理解が早いね。さて、これからがボールの挙動を示す部分だ。ボールの横向きの速さは一定だから、x軸はループのステップごとにVxを加えた値つまり x = x + Vxとなる。

では、上下方向はy = y + Vyですか？でもこれだと、下に落ちてこないですね。このままでは、宇宙まで届いてしまう。

漫画でもない限り、そんなことはないよね。今回は重力による上方向への影響は時間とともに1ずつ減っていくとしよう。つまり各ステップごとにVy = Vy – 1となる。。

初速度が5だったから、ループを回ってこの命令を実行する度に速度が小さくなっていくというわけですね。そして、値がマイナスなると、地面に落ちてくるというわけですね。

その通り。それで、放物線を描いてボールが落ちてくるんだ。

それで地面についたら処理終了という事ですね。

プログラムの実装

# 初期位置 (x, y) を(0, 0)に設定します
x = 0
y = 0

# 初期速度 (VX, vy) を (5, 5) に設定します
Vx = 5
Vy = 5

# シミュレーション時間を300ステップとします。1ステップごとに以下の処理を行います。
for t in range(300):
    # 現在位置 (x, y) を出力します
    print("(", x,",", y, ")")
    
    # 横方向の位置xに横方向の速度Vxを加えて更新します
    x = x + Vx
    
    # 縦方向の位置yに縦方向の速度\Vyを加えて更新します
    y = y + Vy
    
    # 縦方向の速度Vyから1を引いて重力の影響を表現します
    Vy = Vy - 1
    
    # もしyが0以下（地面に到達）したらループを抜けます
    if y <= 0:
        break

# 最終的な位置 (x, y) を出力します
print("(", x, ",", y, ")")

さて、いよいよ今のアルゴリズムをPythomでプログラミングするよ。まず、最初の部分でボールの初期位置xとy、初速度VxとVyを定義する。

アルゴリズムと同じですね

次に”for カウント変数 in range(回数):“で、ループを回すよ。for文は覚えているかな？

はい。アルゴリズムの実装の授業で詳しく説明してもらいましたから、覚えてます。

良いね。今回カウント変数はtで、回数は300回だから”for t in range(300):“で良いね。

ここまではばっちりです。

print(“(“, x,”,”, y, “)”)　の命令で(x、y)の形式で各座標を表示しているんだ。ループでここを通るたびに表示されるよ。少し複雑だけど、ダブルコーテーションで囲った部分はそのまま表示されて、コロンで変数と繋ぐことで、好きな形式で出力できるよ。

なるほど、”(“とか”,”とかって、そのような見た目で表示するために指定しているというわけですね。

その通り、その後で、いよいよボールの挙動だ。アルゴリズムのところですでにモデルは次のように決めていたよね。
x = x + Vx
y = y + Vy
Vy = Vy – 1

重力の影響も考慮してVyはステップ毎に-1しているんだね。

 次に

if y <= 0:

 break

のところで、yが0以下になった時点でループから抜ける条件を設けているよ。これは、地面にボールが接触したときにシミュレーションを終了するためのものだ。

なるほど、if文は「もし～ならば」の条件付き処理を書くためのものでしたね。でも、その後の”break”は何を意味しているんですか？

break文は、ループを強制的に終了するための命令だよ。ここでは、もしが0以下になったら、forループを終了する、という意味になるよ。

それで、ボールが地面に当たると、終了するわけですね。

シミュレーションの実行

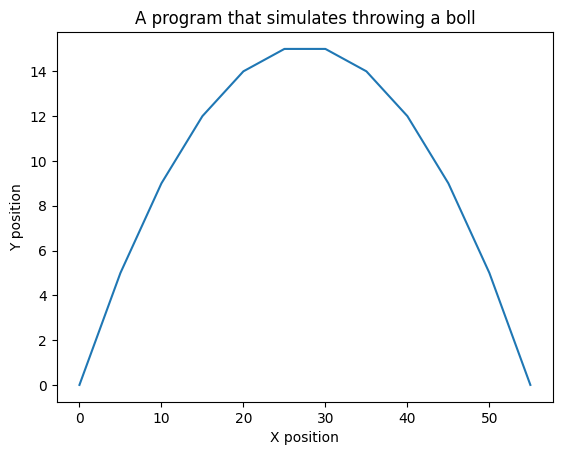
早速プログラムを、実行してみよう。ホールの座標が（x,y)の形式で表示されるはずだよ。

出てきました。(0,0)から始まり、ボールの軌跡が数字で表されているんですね。

ここで出力された値を方眼紙などに書けば、ボールがどのように動いたかを確認できるよ。

なるほど、シミュレーションができたら、どの方向にどのくらいの力で投げれば、一番遠くに届くかわかりますね。

そうだよ。実際にボールを投げて実測するのは時間もお金もかかるから、こうしてシミュレーションして、 問題解決を図るんだ。

はい、ボール投げっぱなしでは体力も持たないので、シミュレーションでVxと、Vyをいろいろと変えて試してみます。

そうだね。得られた結果をもとにモデルの検証をすることも重要だよ。

はい！でも、方眼紙に書くのはちょっとつらいかも。コンピュータが実際にグラフを書いてくれるといいなぁ。

それには、もう少し高度な実行環境が必要なんだ。googleアカウントを持っていれば、Google Colaboratory という実行環境が使えるよ。使い方とソースコードを載せたので、試してみてね。

やってみます！

Pythonプログラム

グラフ描画用Pythonプログラム

import matplotlib.pyplot as plt

# 初期位置を設定
x = 0
y = 0

# 初期速度を設定
VX = 5
vy = 5

# 初期時間を設定
t = 0

# 位置を保存するためのリストを初期化
x_values = []
y_values = []

# 300時間ステップまでシミュレーションを行う
while t < 300:
    # 現在の位置を保存
    x_values.append(x)
    y_values.append(y)

    # 水平方向の速度は一定なので、水平位置を更新
    x = x + VX

    # 垂直方向の速度は時間と共に減少するので、垂直位置と速度を更新
    y = y + vy
    vy = vy - 1 

    # ボールが地面（y=0）に達したら、ループを終了
    if y <= 0:
        break
    
    # 時間を更新
    t=t+1

# 最終的な位置を保存
x_values.append(x)
y_values.append(y)

# 保存した位置データを用いてボールの軌道を描画
plt.plot(x_values, y_values)

# グラフのラベルとタイトルを設定
plt.xlabel('X position')
plt.ylabel('Y position')
plt.title('A program that simulates throwing a ball')

# グラフを表示
plt.show()

Google Colaboratory実行方法

Google Colaboratory（通称：Colab）は、Googleが提供するPythonの実行環境です。Webブラウザ上でコードを直接実行し、結果を即座に確認することが可能です。

以下に、Google Colabを使ってPythonプログラムを実行するためのステップを説明します。
なお、以下の手順は既にGoogleアカウントを持っていることを前提としています。Googleアカウントがない場合には、Googleアカウント作成ページにアクセスしてアカウントを作成してください。

1. Google Colabを開く まず、お手持ちのWebブラウザでGoogle Colabのウェブサイトにアクセスします。そのURLは https://colab.research.google.com/ です。

2. 新しいノートブックを作成する Google Colabのページが開いたら、右上にある「ファイル」メニューをクリックし、「新規ノートブック」を選択します。新しいタブでノートブックが開かれます。

3. Pythonコードを書く 新しいノートブックが開かれると、セルと呼ばれる矩形の領域が表示されます。ここにPythonのコードを書きます。上記の「グラフ描画用Python」を全文コピー＆ペーストしてください。

4. コードを実行する Pythonコードのペーストができたら、セルの左側に表示される再生ボタン（▶︎）をクリックします。すると、その下にコードの実行結果が表示されます。また、キーボードショートカットとしてShift + Enterも利用できます。

5. セーブと共有 作業が終わったら、ノートブックを保存しましょう。左上の「ファイル」メニューから「保存」を選択するか、「ドライブにコピーを保存」を選択して、Google Driveにノートブックを保存します。また、「共有」ボタンから他の人と共有することも可能です。

以上がGoogle Colabを使ってPythonプログラムを実行する基本的な流れです。初めて使う場合は、いくつかの機能に慣れるまで少し時間がかかるかもしれませんが、使えば使うほど、その便利さを実感できるので、ぜひトライしてみてください。

まとめ

名言解説

眞鍋淑郎は日本出身の気象学者・気候学者で、2021年にノーベル物理学賞を受賞しました。彼は主に気候モデルの研究に携わり、特に地球温暖化に関する研究で第一人者とされています。彼が開発した数値モデルは世界中の研究機関で使用され、気候変動の予測に大いに貢献しています。
この名言は、約60年にわたる研究生活の中で彼が持ち続けた「好奇心」を強調しています。彼の長い研究キャリアを通じて、彼は常に新しい発見を求め、理解を深めるために疑問を持ち続けました。これは科学者としての重要な特性であり、彼の業績を支えてきました。
学問は決して終わりがない冒険であり、新しい知識や理解を求める好奇心があれば、どんな困難も乗り越えられます。モデルやシミュレーションを学ぶ過程で難しさを感じるかもしれませんが、それは新しい発見への一歩と考えてください。好奇心を持ち続け、質問を恐れず、一緒に新しい世界を探求しましょう。

問題

「クイズをスタート」のボタンをクリックすると、５問出題します。さあチャレンジ！

編集者ひとこと

いよいよプログラミングも本格的になってきました。文字だけの結果では寂しいので、Google Colaboratoryを使ったグラフ表示のやり方も紹介しました。試してみてくれましたか？

このPythonプログラムではmatplotlibというグラフ描画ライブラリを使用していますが、このライブラリはAIの研究者も使っている本格的なものなので、これらの環境を使ってみることは、AI研究者の入り口に立ったということでもあります。ぜひトライしてみてくださいね。