本日の授業では、データの整理と修正について学びます。データ分析において、欠損値、異常値、外れ値の意味やその処理方法を理解することは非常に重要です。これらのデータは分析結果に大きな影響を与えるため、適切な処理が求められます。
今回は、これらの値の意味を理解し、PythonプログラムのDataFrameを使って、外れ値を算出してみます。
黒板
授業
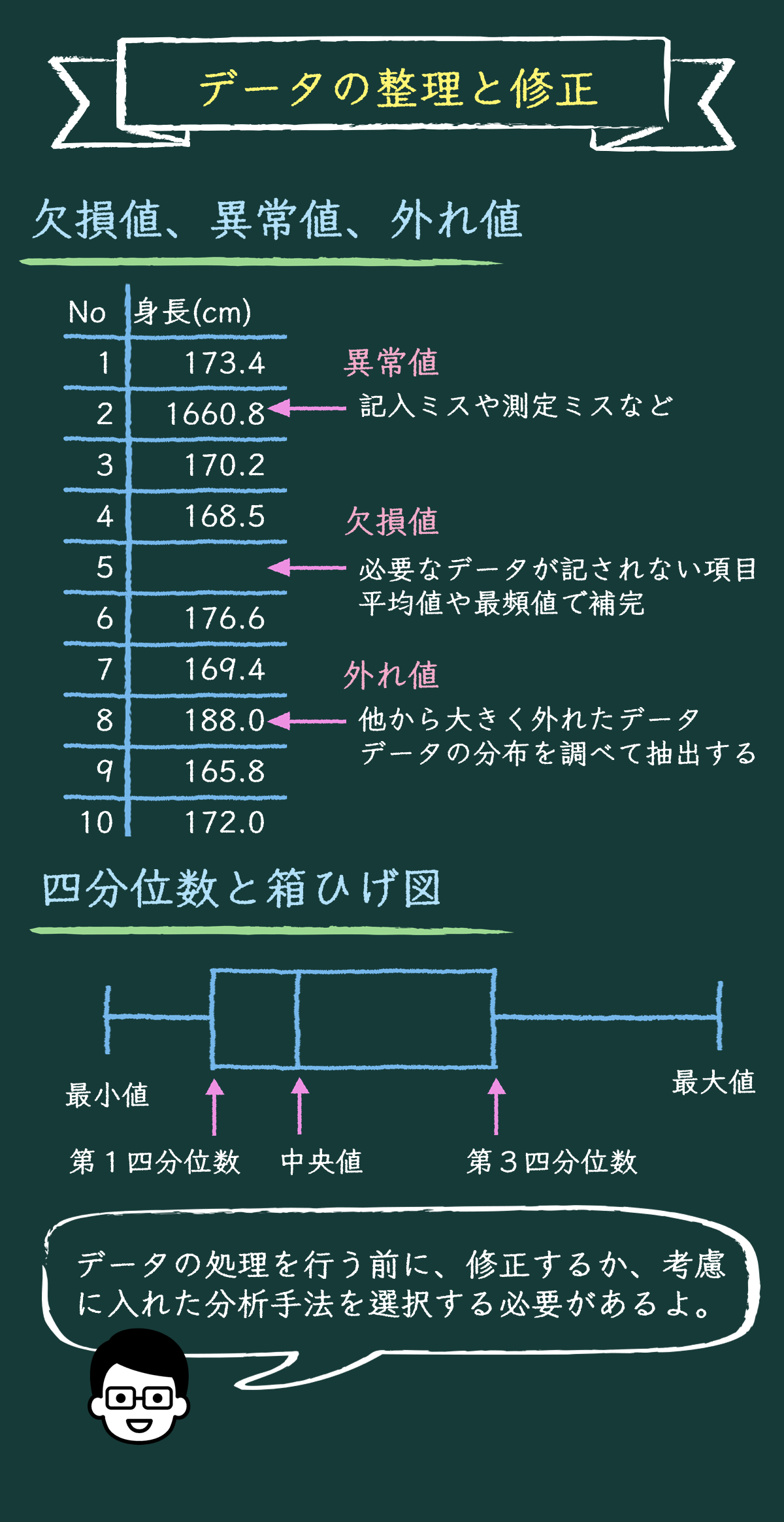
欠損値の処理方法

収集したデータは多くの場合、完全ではないんだ。欠損値って聞いたことあるかな?

値が欠けているということ?

そう。欠損値はデータが欠けている部分のことを言うんだ。例えば、アンケートで回答が抜けている場合などだね。

よくあるよね。でも、どうやって処理するの?

一般的な方法は、他のデータから平均値を使って補完したり、最頻値や中央値で補う方法があるんだ。でも、場合によっては欠損値を無視することもあるよ。

でも、元のデータを変更していいの?データ偽造にならないの?

良い疑問だね。確かに、欠損値を補完することでデータの一部が人工的に作られるわけだから、気をつけなければならない。でも、統計的にはこれが妥当な方法なんだよ。

統計的に妥当ってどういうこと?

例えば、平均値で補完する方法は、そのデータセット全体の傾向を反映するんだ。だから、補完されたデータも全体の傾向に一致するようになるんだよ。

なるほど。データ全体の傾向を見て補完するってことですね。
異常値のスクリーニング

次に異常値について話そう。異常値は他のデータと比較して異常な挙動を示すデータのことを指すんだ。

へぇー、例えばどんなのがあるの?

例えば、データを取得した機器の故障や、入力ミスなんかで、明らかに変な値が収集された場合は、異常値と言えるよね。

そんなのはどうやって見つけるの?

統計手法を使うんだ。箱ひげ図や標準偏差を用いて異常値を検出する方法があるよ。異常値はデータのエラーや特殊なケースを反映していることがあるから、特に注意が必要だね。

なるほど、異常値も無視できないんですね。
外れ値の処理方法

最後に外れ値について説明するね。外れ値は異常値と似ているけれど、必ずしもデータエラーではなく、重要な情報を含んでいることがあるんだ。

じゃあ、外れ値はどうやって判断するの?

外れ値はデータの分布を見て、他のデータと比べて極端に外れている値だね。異常値のところでも出てきたような箱ひげ図などの統計手法や、回帰分析を使って予測値から大きく外れているデータを外れ値として検出することがあるんだ。

でも、外れ値を見つけたらどうするんですか?

外れ値がデータエラーでない場合、そのまま保持することもあるし、分析の目的に応じて除去することもあるんだよ。どちらにせよ、外れ値の発生原因をよく理解することが重要だね。

データ分析って奥が深いですね。
【実習】Pythonプログラムによる外れ値の抽出
Pythonプログラム
# 学生の身長データの分析
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 生徒の身長データを辞書型で定義
data = {
'StudentID': range(1, 11), # 学生IDを1から10までの範囲で生成
'Height': [173.4, 166.8, 170.2, 168.5, 172.0, 176.6, 169.4, 167.2, 165.8, 188.0] # cm単位の身長データ
}
# データをDataFrameに変換
df = pd.DataFrame(data)
# 生徒の身長データを表形式で表示
print("\n身長データ:")
print(df.to_string(index=False)) # インデックスを表示せずにデータフレームを出力
# 生徒の身長データの基本統計量を計算
median = df['Height'].median() # 中央値を計算
Q1 = df['Height'].quantile(0.25) # 第1四分位数を計算
Q2 = median # 第2四分位数は中央値と同じ
Q3 = df['Height'].quantile(0.75) # 第3四分位数を計算
IQR = Q3 - Q1 # 四分位範囲(IQR)を計算
# 統計量を出力
print("\n統計量:")
print(f" 中央値 (Median): {median}")
print(f" 第1四分位数 (Q1): {Q1}")
print(f" 第2四分位数 (Q2): {Q2}")
print(f" 第3四分位数 (Q3): {Q3}")
print(f" IQR: {IQR}")
# IQRを使用して外れ値を検出
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers = df[(df['Height'] < lower_bound) | (df['Height'] > upper_bound)]
print("\n外れ値 (Outliers):")
print(outliers) # 外れ値のデータを表示
# 生徒の身長データの箱ひげ図を作成
plt.figure(figsize=(10, 6)) # 図のサイズを指定
sns.boxplot(x=df['Height']) # Seabornを使用して箱ひげ図を作成
plt.title('Box Plot of Heights') # 図のタイトルを設定
plt.xlabel('Height (cm)') # x軸のラベルを設定
plt.show() # 図を表示
Google Colaboratoryとは

じゃあ、実際にPythonを使って生徒の身長データを分析してみよう。

なんだか難しそうだけど、興味あるなぁ。

なおや君、今日はGoogle Colaboratoryを使うよ。準備はいいかい?

検索Googleですか?

そうだよ。Google Colabは、インターネットブラウザ上でPythonを実行できる環境なんだ。GoogleのアカウントさえあればOKだ。

なるほど、Googleアカウント持っているで、早速やってみます。
Pythonプログラムコードの入力

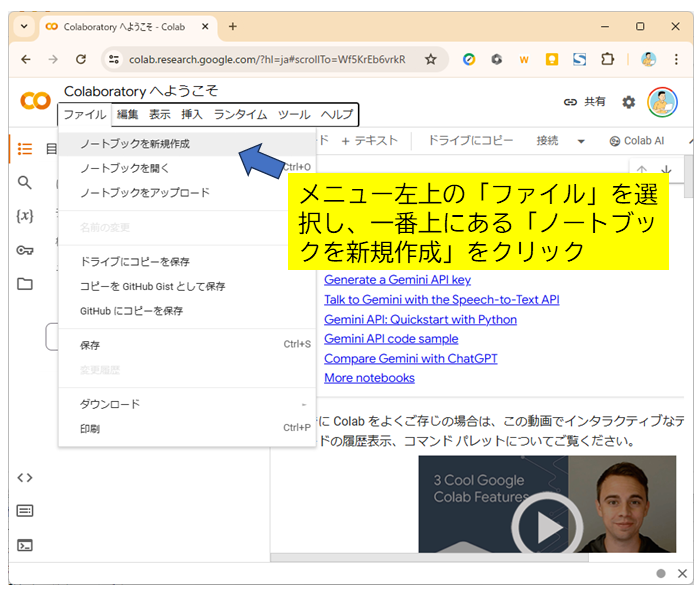
まずはGoogle Colaboratoryにアクセスして、新しいノートブックを作成しよう。メニュー左上の「ファイル」を選択し、一番上にある「ノートブックを新規作成」をクリックしてみて。

了解です!新しいノートブックを作成しました。
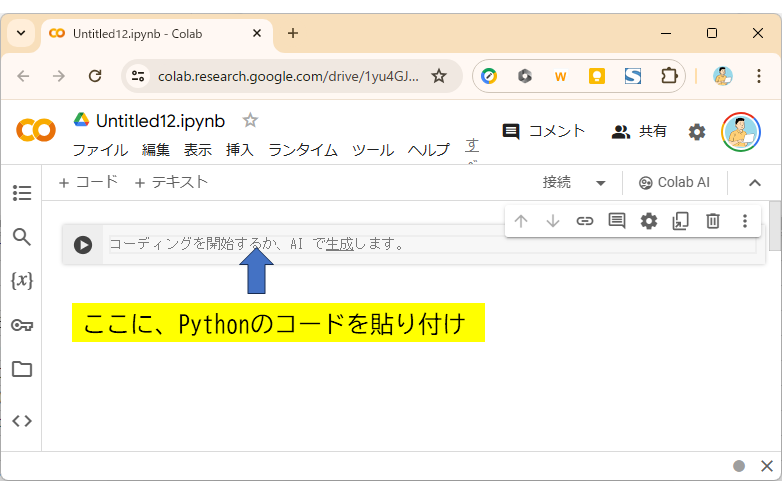

では、Pythonプログラムをコピペして入力しよう。コードは先ほど示したのもをコピーしてね。ソースコードの右上にあるアイコンをクリックするとコピーできるので、三角のボタンの右側で、Ctrl+V(MACはcommand + V)を押してね。

コピペで良いんですか?
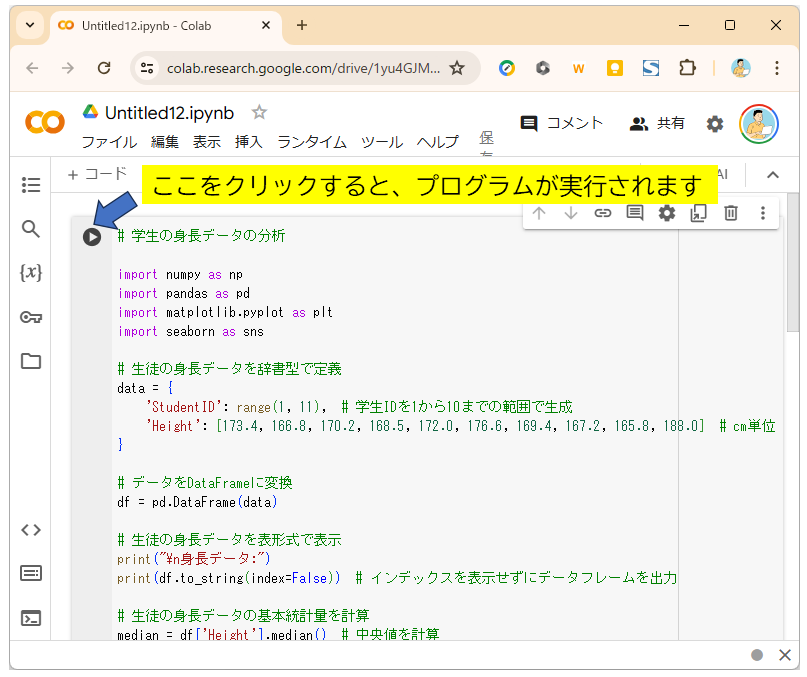

コードの中身は後で説明するから、まずは実行してみよう。

はい、何事も実行ですね。
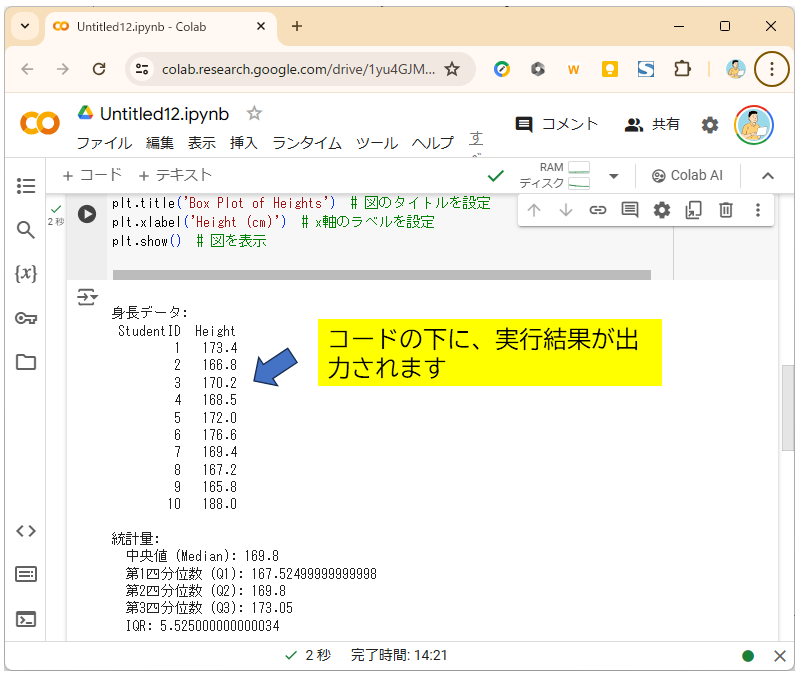
実行結果
実行結果の確認(第1四分位数、第3四分位数)

Google Colaboratoryの結果は上のグラフか、ここをクリックすると表示されるから見てね。どんな結果が表示されたかな?

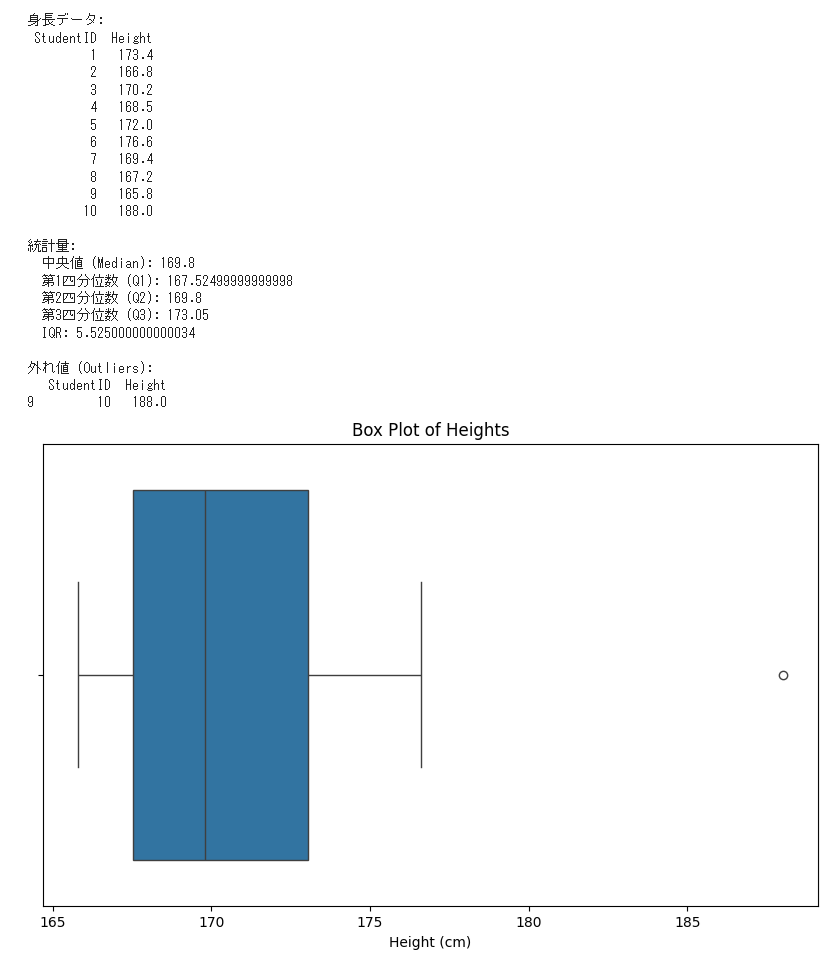
まず、身長データ、統計量、外れ値、それに見慣れないグラフです。

まずは統計量のところから見ようか。中央値はデータを小さい順に並べたときの真ん中の値だよ。

これだけはわかる。中央値と平均値とは違うんですよね。中学で習いました。

そして、第1四分位数(Q1)はデータの下位25%、第3四分位数(Q3)は上位25%のことを指すんだ。

第1四分位数?。何が何だかさっぱりわかりません。

もちろんだよ。データを小さい順に並べたとき、下位から25%の位置にある値が第1四分位数、略してQ1、下位から75%の位置にある値が第3四分位数、略してQ3なんだ。

なるほど。データを4つに分けたときの境界みたいな感じですか?

その通りだよ。ちなみに第2四分位数(Q2)というのもあって、これは中央値の事を意味するんだ。
実行結果の確認(外れ値)

もうひとつIORというものが出力されてますが、これは何ですか?

IQRは「Interquartile Range」の略で、四分位範囲という意味だ。先ほどの、第3四分位数(Q3)から第1四分位数(Q1)を引いた値だよ。これはデータの中央50%の範囲を示しているんだ。

なるほど、でもなんでこんな面倒な値を求めるんですか?

外れ値を見つけるためだよ。IOR法では、ある値が、Q1から1.5倍のIQRを引いた値よりも小さいか、Q3から1.5倍のIQRを足した値よりも大きければ、外れ値として定義されるんだ。

うーん、普通の値ではなところを求めるための計算であるということはわかったのですが、ちょっとイメージわきません。
箱ひげ図
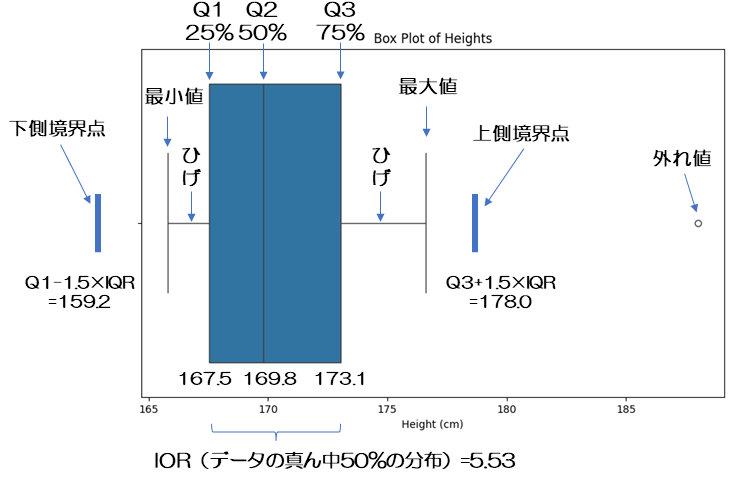

この下のBox Plot of Heightsというグラフを見るとイメージがつかみやすいと思う。これを箱ひげ図というんだ。

箱ひげ?どうやって見るんですか?

箱ひげ図はデータの分布を視覚的に表現するためのグラフなんだ。まず、箱の部分はデータの真ん中50%、つまりIQRの範囲だよ。

なるほど。箱の中に50%の人の身長が収まっているんですね。じゃあ、箱の左右に伸びている線は何ですか?

それは「ひげ」と呼ばれていて、データの範囲を示しているんだ。左側が外れ値を除いた観測値の下限、右側が外れ値を除いた観測値の上限だよ。

うーん、でもさっき外れ値の求め方で説明してもらった、Q3から1.5倍のIQRを足した値というのはどこに表示されているんですか?

実は、通常箱ひげ図には表されていないんだ。上の表では、わかりやすいように「上側境界点」や「下限境界点」として表したよ。

なるほど。Q3×1.5×IQRというところですね。

その通りだよ。この場合、身長188cmのデータ点が「〇」印で、外れ値として表示されているね。

箱ひげ図を使うと、データの分布や外れ値が一目でわかるんですね。
Pythonプログラムの確認(DataFrame)

じゃあ、プログラムを見てみよう。身長のデータはどこで定義しているかな?

「# 生徒の身長データ」のところで、data という変数に、身長らしいデータを代入しているようには見えるけど・・・。
# 生徒の身長データ
data = {
'StudentID': range(1, 11),
'Height': [173.4, 166.8, 170.2, 168.5, 172.0, 176.6, 169.4, 167.2, 165.8, 188.0] # cm
}
df = pd.DataFrame(data)
そうだね、そして、df = pd.DataFrame(data) というところで、DataFrameに変換して、変数dfに代入しているんだ。

うーん。DataFrameって何ですか?

DataFrameは、Pythonでよく使われるpandasというライブラリで使われるデータ構造の一つなんだ。

パンダっす?

表形式のデータを扱うためのもので、Excelシートみたいなものだと思ってくれればいいよ。

Pythonプログラムの確認(統計量の計算)
# 基本統計量の計算
median = df['Height'].median()
Q1 = df['Height'].quantile(0.25)
Q2 = median
Q3 = df['Height'].quantile(0.75)
IQR = Q3 - Q1
dfって変数に表の形式でデータが入っているってことはわかったんだけど、df[‘Height’]って何を示すの?

このように示すことで、DataFrameの中の特定の列を参照できるんだよ。たとえば、df[‘Height’]と書くと、DataFrameの中のHeightという列のデータ全てを示しているんだ。

じゃあ、median = df[‘Height’].median()ってどういう意味になるの?

これはHeight列に含まれるデータ全てから中央値を計算しているんだ。median()という関数が中央値を求めるための関数なんだよ。

Q1 = df[‘Height’].quantile(0.25)は、さっきmedian()だったところが、quantile(0.25)に変わっているね

quantile()という関数は、データの特定の分位点を計算するための関数なんだ。0から1の間の値を指定することで、その位置の値を返してくれるんだよ。

なるほど、0.25を指定すると、Q1の値が得られるですね。

その通りだよ。そして、同じ方法で第3四分位数(Q3)も計算できるんだ。

Q1から1.5倍のIQRを引いた値が下限、Q3から1.5倍のIQRを足した値を上限として、そこから外れた値が外れ値ですね。

良いね。じゃあ、次に外れ値を検出するためのコードを見てみよう。この部分のコードだよ。
Pythonプログラムの確認(下側境界、上側境界の算出)
# IQRを使った外れ値の検出
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
何やら計算してますね。

箱ひげ図のところで、下側境界点とか、上側境界点という話をしたよね。ここでlower_bound は下側の境界点の事だよ。

なるほど。lower_bound = Q1 – 1.5 * IQRというのは、Q1から1.5倍のIQRを引いた値よりも小さいデータ点という意味か!

そう。下限と上限を定めれば、DataFrameのフィルタリングを使って外れ値を求められるんだ。

次々と謎な言葉が出てきます。フィルタリングって何ですか?

つまり、データの中から特定の条件に合う行だけを抽出することなんだ。

ふむふむふむ。DataFrameというのは、本当にエクセルみたいですね。どうやって書くんですか?
Pythonプログラムの確認(外れ値の検出)
outliers = df[(df['Height'] < lower_bound) | (df['Height'] > upper_bound)]
ここで、df[‘Height’] < lower_boundというところで、データの中から下側境界値(lower_bound)より小さいデータを抽出している。

なるほど。じゃあdf[‘Height’] > upper_bound)のところで、上側境界値より大きいデータが抽出できるわけですね。

その通り、|の記号は論理演算子の「または」の意味で、この2つの条件のどちらかを満たす行を抽出して、outliersというDataFrameに代入しているんだ。

つまり、外れ値になるデータを選び出しているんですね。

その通りだよ。結果として、外れ値を含む新しいDataFrameが作成されて、それがoutliersという変数に格納されるんだ。

へえ、こうやって外れ値を見つけるんですね。DataFrameを使うと、データの操作が簡単になるんですね。

そうだね。DataFrameはとても便利なデータ構造だから、これからもいろいろな場面で使っていくよ。しっかり覚えておいてね。

pythonのコードは、まだまだ消化不良ですが、雰囲気はわかった気がします。

そうだね。Pythonはツールとして使えればよいよ。実際に使っていくうちに理解できてくるから安心していいよ。

はい、頑張ります
まとめ
- 欠損値の概念
欠損値とは、データセット内で欠けているデータの部分を指します。アンケートの未回答部分などが該当します。 - 欠損値の処理方法
欠損値の処理方法には、平均値や最頻値で補完する方法があります。場合によっては、欠損値を無視することもあります。 - 異常値の定義
異常値は、データセット内で極端に大きいか小さい値を指し、統計手法を用いて検出されます。箱ひげ図や標準偏差を使って見つけます。 - 外れ値の処理方法
外れ値は、データの分布から大きく外れた値で、必ずしもエラーではなく重要な情報を含むことがあります。外れ値の処理方法は分析の目的に応じて異なります。 - 外れ値の発生原因
外れ値は、データ収集の方法やデータの品質に問題がある場合に発生することが多いです。原因を特定し、適切に対処することが重要です。
名言解説
Data is the new oil” – Clive Humby
クライヴ・ハンビ(Clive Humby)は、イギリスの著名なデータサイエンティストであり、データ分析と顧客関係管理の分野で広く認識されています。
「データは新しい石油だ(Data is the new oil)」というクライヴ・ハンビの名言は、2006年に初めて発言されました。このフレーズは、現代社会におけるデータの価値とその潜在能力を強調しています。石油が20世紀の産業革命を支えた重要な資源であったように、データは21世紀の情報革命を支える重要な資源であるという意味が込められています。ハンビの言葉は、データが適切に収集、整理、分析されることで、企業や社会にとって非常に価値のある資産となることを示しています。
この名言には、後の人たちにより次のような補足が加えられています。
「Data is the new oil, but like oil, it must be refined before it can be of use(データは新しい石油だが、石油のように、使えるようになるには精製されなければならない)」。
データの価値がそのままではなく、加工や分析によって初めて有用な情報となることを強調しています。さらに、データの収集だけではなく、その後の処理、特にスクリーニングの重要性を強調しています。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジ!
編集者ひとこと
データ分析を始める前に、まずやらなければいけないのが、欠損値や異常値、外れ値の処理です。こういった泥臭い作業があってはじめて、ちゃんとしたデータ分析ができます。
データ分析の実際をイメージしてもらいたくて、今回はPythonを使ってみました。ちょっと難しいかもしれませんが、まずは実践。実際にGoogle Colaboratoryを使ったデータ分析にチャレンジしてみて下さい。
<RANKING>![]()
高校教育ランキング