今日はデータ分析について勉強します。特に、東京都の年間降雨量データを使って度数分布表を作成し、ヒストグラムを作成します。度数分布表の階級、階級の幅、度数、階級値などについても説明します。データの分布を視覚化することで、データの傾向や特徴を理解する方法を学びましょう。さらに、正規分布との比較を通して、データの特徴を詳しく分析し、標準偏差の役割についても学びます。
黒板
授業

度数分布表って聞いたことあるかな?

うーん、なんとなく聞いたことはあるけど、具体的にはよくわかんないな。

なるほどね。度数分布表は、データを区間に分けて、その区間にどれだけのデータが含まれるかを表にまとめたものなんだよ。

ふーん、データを整理するための表ってことか。
度数分布表の作り方

そうだね。じゃあ、具体的にどうやって作るかを見ていこう。まず、データをいくつかの区間に分けるんだ。これを「階級」って言うよ。

階級?それってどうやって決めるの?

いい質問だね。階級の決め方はデータの範囲や数によって変わるけど、一般的にはデータの最大値と最小値を基に適切な間隔で分けるんだ。例えば、10から50までのデータがあるときに5ずつ区切るとかね。

なるほど!なんか細かい作業だね。でも、そうするとデータが整理されて見やすくなるんだね。
ヒストグラムとは

次にヒストグラムについて説明しよう。ヒストグラムは、度数分布表を視覚的に表現したグラフなんだ。

グラフかー。具体的にはどうやって描くの?

まず、度数分布表の各階級を横軸に取って、その階級の度数を縦軸に取るんだ。それを棒グラフの形で描くんだよ。

あー、なんとなく見たことあるかも。棒グラフでデータの分布が一目でわかるんだね。
ヒストグラムの作り方

じゃあ、具体的にヒストグラムを描いてみよう。今回は、気象庁のデータから東京都の年間降水量データを用いるよ。(リンク先 → 東京都 降水量 過去データ)

1876年からデータがあるんだね。どうやって始めればいいの?

まず、このデータを階級に分けるところから始めるよ。今回は階級の幅を200mmにするよ

なるほど!200mm区分で、発生した年の数をカウントして棒グラフにしていくんだね。

その通り。手でカウントしていくのは大変だから、パソコンで処理させよう。

賛成!このデータどうやって保存できるのかな?

エクセルなどに張り付けで保存すればよいよ。私の方で保存しておいたファイルがあるから、ダウンロードしてみてね。(ダウンロード tokyo_rainfall.csv)

はい、PCのダウンロードフォルダに保存されました。
Google Colaboratoryによるグラフ描画

今回もGoogle Colaboratoryを使ってグラフを作ってみよう。Google Colaboratoryについては、前回(45.データの整形と修正)詳しく解説しているので、はじめてのまずそちらから見てね。

了解!じゃあ、「新しいノートブックを開く」ですね

その通り。今回はまず、先ほどのデータファイルをGoogle Colaboratoryにアップロードしてみよう。

アップロードってどうやるの?

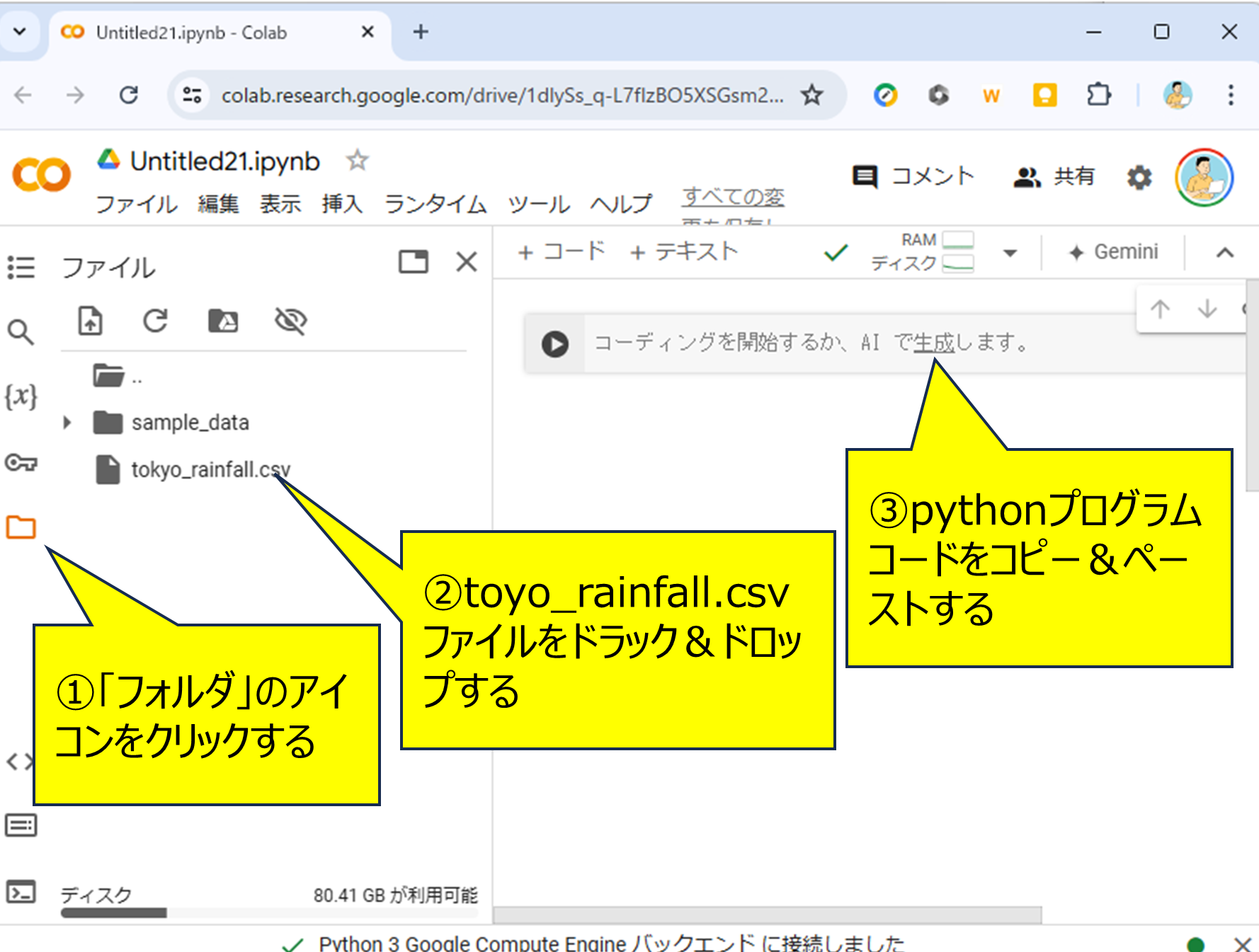
簡単だよ。画面の左側にある「フォルダ」のマークをクリックすると、サイドバーが表示されるので、そこに、先ほどダウロードした、tokyo_rainfall.csv ををドラッグ&ドロップすればよいんだ。

はい、sample_dataという表示の下に、rainfall.csvという表示が追加されました。

良いね。それでは、次のpythonプログラムを、コピーして、右側のウィンドウの三角マークの隣にペーストして。
Pythonプログラム
import pandas as pd # データ操作用ライブラリ
import matplotlib.pyplot as plt # グラフ描画用ライブラリ
import numpy as np # 数値計算用ライブラリ
import scipy.stats as stats # 統計計算用ライブラリ
# CSVファイルの読み込み
file_path = '/content/tokyo_rainfall.csv' # Google Colabでのファイルパス
data = pd.read_csv(file_path, encoding='shift_jis') # 日本語文字エンコーディングの指定でCSVファイルを読み込む
# 年間降水量の値をリストに変換
annual_rainfall = data['value'].dropna().tolist()
# 統計量の計算
n = len(annual_rainfall)
max_value = max(annual_rainfall)
min_value = min(annual_rainfall)
mean = np.mean(annual_rainfall)
median = np.median(annual_rainfall)
std = np.std(annual_rainfall)
# 統計量の表示
print(f'Number of data points: {n}')
print(f'Max value: {max_value} mm')
print(f'Min value: {min_value} mm')
print(f'Mean: {mean:.2f} mm')
print(f'Median: {median} mm')
print(f'Standard Deviation: {std:.2f} mm')
# ヒストグラムの作成(ビンの幅を100mmに設定)
plt.figure(figsize=(10, 6))
count, bins, ignored = plt.hist(annual_rainfall, bins=range(int(min(annual_rainfall)), int(max(annual_rainfall)) + 100, 100), edgecolor='black')
# 正規分布曲線の作成
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, mean, std) * len(annual_rainfall) * (bins[1] - bins[0])
plt.plot(x, p, 'k', linewidth=2)
# グラフのラベルとタイトルの設定
plt.xlabel('Annual Rainfall (mm)') # X軸のラベルを設定
plt.ylabel('Frequency') # Y軸のラベルを設定
plt.title('Histogram of Annual Rainfall in Tokyo with Normal Distribution (Bin width: 100mm)') # グラフのタイトルを設定
plt.grid(True) # グリッドを表示
plt.show() # グラフを表示
えっ?こんな難しそうなプログラムを実行するの?

うん、グラフ描画用のライブラリなども使っているから、ちょっと難しいかもね。詳しい解説は、#マークの後のコメントに記しているので、興味があったら読んでみてね。

じゃあ、まずは実行。おっ、何か数字と、グラフが出てきた。
データの詳細説明

Google Colaboratoryの結果は上のグラフか、ここをクリックすると表示されるから見てね。
じゃあ、得られた結果を分析してみよう。

はい、先生。まずはどこから始めるんですか?

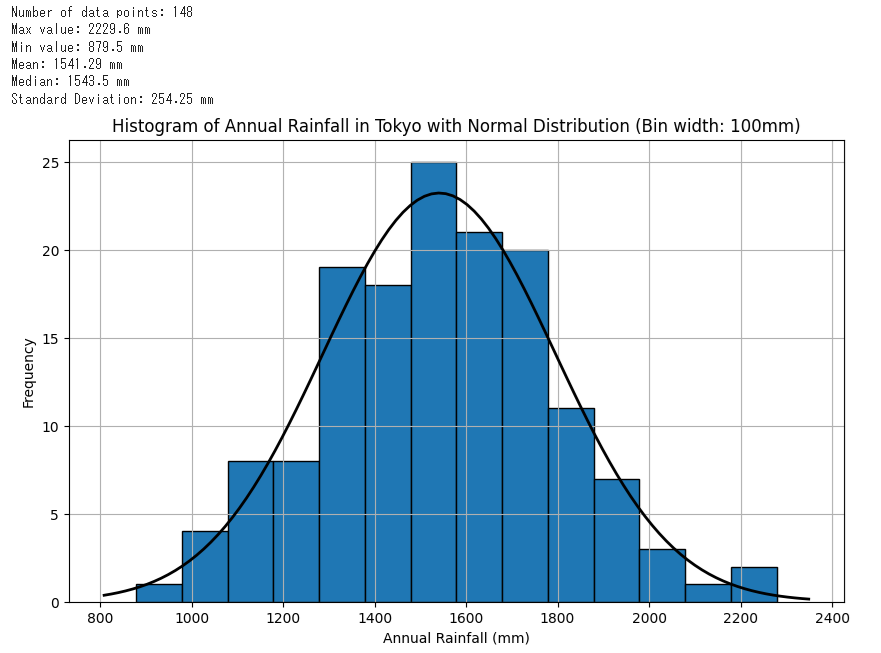
まず、データの基本的な統計量を見てみよう。データの数(Number of data points)、最大値(Max value)、最小値(Min value)、平均(Mean)、中央値(Median)、標準偏差(Standard Deviation)を計算してみたよ。

おお、それはすごいですね。どんな結果が出たんですか?

データの数は 148 点、最大値は 2229.6 mm、最小値は 879.5 mm、平均は 1541.29 mm、中央値は 1543.5 mm、標準偏差は 254.25 mm だよ。

グラフを見ると、ちょうど左右対称に見えますね。

良いね。中央値と平均がほぼ同じってことは、このデータは偏りが少ないってことを示している。

こうしてグラフにすると、データの分布のイメージが付きやすいですね
ヒストグラムと正規分布

そうだね。さらに正規分布を利用すると、統計を利用した分析も行えるようになるんだ。

正規分布?

平均値と最頻値・中央値が一致し、それを軸として左右対称となっている確率分布の事だよ。今回はヒストグラムの上に重ねて表示しているよ。

このベルのような形の、線でかかれたグラフですね。確かに、ヒストグラムと近い形をしています。

そうだね。こういった、自然現象の長期データは、正規分布に従う場合が多いんだ。

なるほど、でも正規分布に近いと何かいいことあるんですか?

良い質問だね。正規分布は、多くの自然現象や測定データに当てはまるから、データ分析や統計解析の基本となるんだ。

それって具体的にはどういうことですか?

例えば、正規分布を仮定することで、平均や標準偏差を使ってデータの特性を簡単に把握できる。さらに、正規分布に基づく統計手法を使うことで、データの傾向や予測を正確に行うことができるんだ。

平均はわかるけど、標準偏差って何ですか?
標準偏差 68-95-99.7則

それじゃあ、標準偏差について説明しよう。標準偏差はデータのばらつき具合を示す指標なんだ。

標準偏差が大きいとどうなるんですか?

標準偏差が大きいとデータが平均から大きく離れていることが多いということだよ。今回のデータでは標準偏差が231.4 mmだから、平均から約231.4 mm以内にデータの多くがあるということだね。

へぇ、そうなんですね!

標準偏差の範囲についてもう少し詳しく説明しよう。標準偏差の事を1σ(シグマ)というんだ。そしてその2倍の値が2σ、3倍が3σといったように表現するよ。

σ(シグマ)ですか。はじめて聞きました。

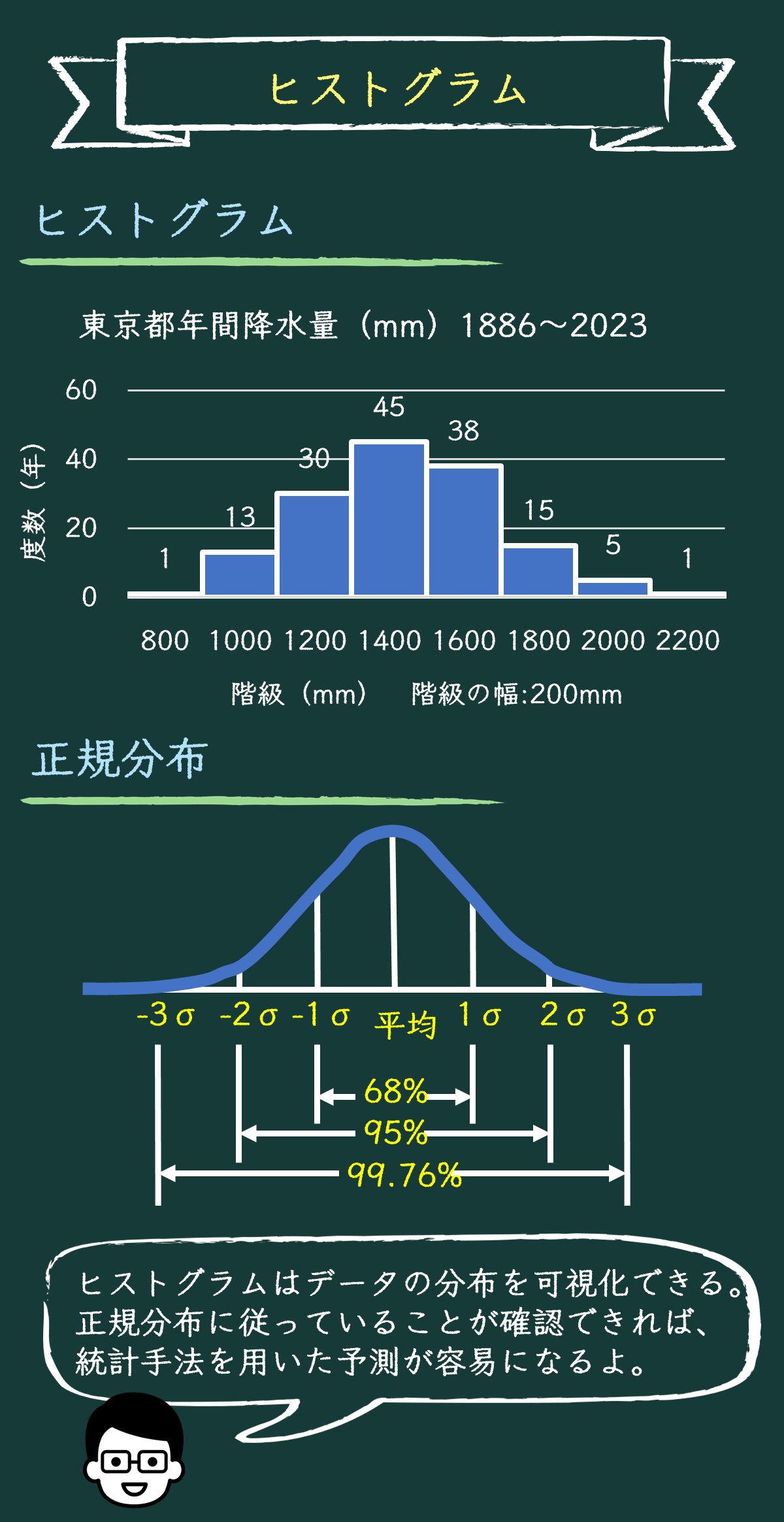
正規分布では、データの約68%が平均±1σの範囲に、約95%が平均±2σの範囲に、約99.7%が平均±3σの範囲に収まるんだ。

むむむ?それ覚えなければいけない数字ですか?

統計学における68-95-99.7則というルールは有名なので、頭の片隅にでも置いておくと便利だよ。

はい、では片隅にしまっておきます

今回のデータで計算すると、平均が1541.29mm、標準偏差(σ)が254.25mmだから、1σの範囲は1287.04mmから1795.54mmになるよね。

つまりは、東京の年間雨量は68%の確率で、この範囲に入るとうことですね。

そうだね。そうだね。そして、2σの範囲は1032.79mmから2049.79mm、3σの範囲は778.54mmから2304.04mmだよ。

じゃあ1984年の年間降雨量879.5mmというのは、2σと3σの中間なので、かなりレアってことですかね。

そうだね。実際に計算すると、879.5mmは平均の1541.29mmから-2.60σ離れている。これは212年に1回の確率ということになる。

なるほど、148年の間には、そんな年が1回くらいあっても不思議ではないですね。
正規分布の活用

正規分布が分かっていると、いろいろな予測が出来そうですね。これって他にも応用できるの?

もちろんさ。例えば、生徒の個々の成績を全体の成績と比較するために、偏差値を使うよね。

はい。あれが、正規分布と関係あるんですか?

そうだよ。偏差値は平均を50として、1σを10にした正規化されたモデルなんだ。つまり、偏差値50が平均で、偏差値60は1σ上、偏差値40は1σ下になるんだよ。

ということは、68-95-99.7則に従うと、68%の人は偏差値40~60の間に入っているという意味ですね。

その通り。別の言い方をすると、偏差値60以上ということは、68%の残りの32%の上の方、つまり上位16%に入るということになるんだ。

じゃあ、偏差値70とかになると、95%の残りの5%のさらに上位だから、2.5%に入るということですね。

その通り。100人いれば2人か3人くらいが偏差値70以上ということになる。

うーん。じゃあ、自分の成績より高い偏差値の大学に合格する確率は低いという現実を知ることになるのですね。

あくまで統計的にということだけれども、成績の分布を正規分布として捉えることで、全体の中で自分の位置がどれくらいかを理解しやすくなるんだ。
まとめ
- 度数分布表
データを一定の範囲に分け、その範囲ごとにデータの数(度数)を数える表である。データの分布を視覚的に把握することができる。 - 階級と階級の幅
階級はデータを分類する範囲であり、階級の幅はその範囲の広さを示す。適切な幅を選ぶことが重要である。 - 度数と階級値
度数は各階級に含まれるデータの数、階級値は各階級の中央の値である。データの代表値として使われる。 - ヒストグラム
度数分布表を視覚的に表現したもので、X軸に階級、Y軸に度数を取って描かれる棒グラフである。 - 標準偏差と正規分布
標準偏差はデータの散らばり具合を示し、正規分布はデータが平均を中心に左右対称に分布する様子を示す。データの約68%が1σ、約95%が2σ、約99.7%が3σの範囲に含まれる。
名言解説
西内 啓の著書である「統計学が最強の学問である」は、シリーズ累計40万部を超え 2014年度ビジネス書大賞を受賞するなど、国内に統計ブームを巻き起こしました。
統計学は、データを分析し、そこから意味のある情報を引き出す方法を提供します。これにより、未知の事象を予測し、問題を解決するための強力なツールとなります。例えば、医療の分野では、統計学を用いて病気の発生率や治療の効果を分析します。ビジネスでは、消費者の行動を予測し、マーケティング戦略を立てる際に活用されます。また、科学研究では、実験結果を解析し、仮説を検証するために欠かせないものです。
統計学を学ぶことで、情報を正しく理解し、客観的に物事を判断する力を身につけることができます。この力は、将来の様々な場面で役立ちます。どんな分野に進むとしても、統計学の知識は大きな武器となります。データに基づいた合理的な考え方を身につけ、自信を持って未来に挑戦していきましょう。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジ!
編集者ひとこと
今回も、Google Colaboratoryを使って、データ分析を実践してみました。普段はエクセルの「データ分析」を使うことが多いのですが、Pythonでの分析も慣れると便利ですね。これらのコードも大半はChatGPTで作っています。さらに、可視化するだけでなく、分析自体もAIがやってくれるので、基本が理解出来たら、AIをうまく活用していろいろなデータを分析してみてください。
<RANKING>![]()
高校教育ランキング