問題
問題文
| 出典:独立行政法人大学入試センター 公開問題「平成30 年告示高等学校学習指導要領に対応した令和7年度大学入学共通テストからの出題教科・科目 情報サンプル問題」 https://www.mext.go.jp/content/20211014-mxt_daigakuc02-000018441_9.pdf |
第2問 次の文章を読み、後の問い(問1 ~ 3)に答えよ。
Mさんは、18歳になって選挙権が得られたのを機に、比例代表選挙の当選者を決定する仕組みに興味を持った。そこで各政党に配分する議席数(当選者数)を決める方法を、友人のKさんとプログラムを用いて検討してみることにした。
次の文章の空欄(ア)~(ウ)に入れる最も適当なものを、後の解答群のうちから一つずつ選べ。同じものを繰り返し選んでもよい。
Mさん: 表1に、最近行われた選挙結果のうち、ある地域のブロックについて、各政党の得票数を書いてみたよ。

K さん: 今回の議席数は6 人だったね。得票の総数を議席数で割ると580人なので、これを基準得票数と呼ぶのがいいかな。平均して1議席が何票分の重みがあるかを表す数ということで。そうすると、各政党の得票数が何議席分に相当するかは、各政党の得票数をこの基準得票数で割れば求められるね。
Mさん: その考え方に沿って政党ごとの当選者数を計算するプログラムを書いてみよう。まず、プログラムの中で扱うデータを図1と図2にまとめてみたよ。配列Tomeiには各政党の党名を、配列Tokuhyo には各政党の得票数を格納することにしよう。政党の数は4つなので、各配列の添字は0 から3 だね。


M さん: では、これらのデータを使って、各政党の当選者数を求める図3のプログラムを書いてみよう。

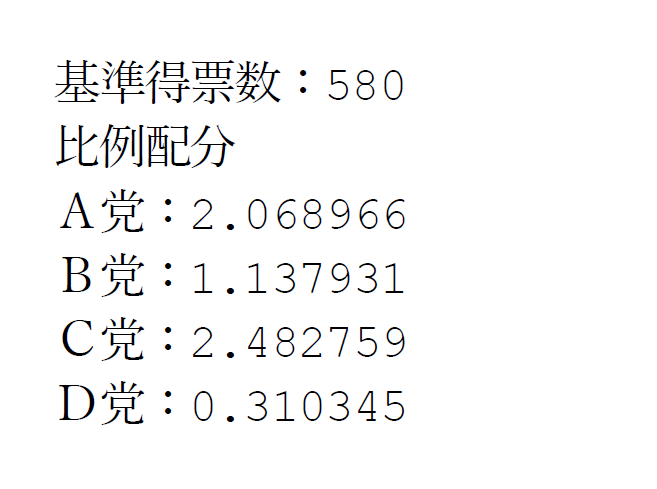
Kさん: 得票数に比例して配分すると小数点のある人数になってしまうね。小数点以下の数はどう考えようか。例えば、A党は2.068966 だから2 人が当選するのかな。
Mさん: なるほど。切り捨てで計算すると、A党は2人、B党は1 人、C 党は2 人、D党は0 人になるね。あれ? 当選者数の合計は5 人で、6 人に足りないよ。
Kさん:切り捨ての代わりに四捨五入したらどうだろう。
Mさん: そうだね。ただ、この場合はどの政党も小数点以下が0.5未満だから、切り捨てた場合と変わらないな。だからといって小数点以下を切り上げると、当選者数が合計で9人になるから3人も多くなってしまう。
Kさん:このままでは上手くいかないなぁ。先生に聞いてみよう。
解答群
| (ア)、(イ)、(ウ)の解答群 | ||
| (0) 0 | (1) 1 | (2) 2 |
| (3) 3 | (4) 4 | (5) 5 |
| (6) 6 | (7) Tomei[m] | (8) Tokuhyo[m] |
| (9) sousuu | (a) giseki | (b) kizyunsuu |
解答
- (ア)の解答 (3) 3
- (イ)の解答 (8) Tokuhyo[m]
- (テ)の解答 (b) kizyunsuu
解説
本日の授業では、プログラミング問題を解く際のコツを伝えます。プログラミング問題には必ずヒントがあります。今回はDNCLのプログラムを通して、ヒントを見つける練習をしていきましょう。
黒板

試験問題回答
試験問題(ア)の解説

Mさん: 配列Tomeiには各政党の党名を、配列Tokuhyo には各政党の得票数を格納することにしよう。政党の数は4つなので、各配列の添字は0 から3 だね。

まず「mを0からアまで1ずつ増やしながら繰り返す」とあるんだけど、この「ア」に入る値が何か考えてみようか。

えっと、どこを見ればいいんでしょうか?

ヒントは(05)行目と(06)行目にあるよ。特に、(06)行目に「Tokuhyo[m]」と書かれているのを見てみよう。ここで使われている「m」は、ループの中で使われている変数なんだ。

なるほど、ループの中で0,1・・と増えていくんですね。でも、mの最大値はどうやって決めるんですか?

このプログラムでは「m」は配列のインデックスとして使われているんだ。Mさんの発言に「政党の数は4つなので、各配列の添字は0から3だね」とあるね。

ヒントはそこか!。mの最大値は3。(ア)は「3」ですね。
試験問題(イ)の解説

K さん: 各政党の得票数が何議席分に相当するかは、各政党の得票数をこの基準得票数で割れば求められるね。

ここでは「比例配分」を表示しようとしているよね。ところが、「比例配分」という言葉は、会話の中に出てきていないよね。

ちょっと待って、Kさんの発言に、得票数を基準得票数で割れば求められるとあるね。だから、(イ)は得票数で、(ウ)は基準得票数かな?

いいところに目を付けたね。でも、日本語のままでは計算できないよ。

確かにそうだね。選択肢からそれらしいものを探すと、得票数はTokuhyo[m]、基準得票数はkizyunsuuかな?山勘だけど!

正解。わかりやすい変数名をつけているから、名前で想像できたね。でも、ちゃんと意味を理解していなければプログラムはかけないよ。

よく見ると、図2にTokuhyo配列の説明があるし、(08)行目のコードで基準得票数をkizyunsuuという変数で表示していますよね。

その通り。なんだ、ちゃんと理解していたんだね。
DNCL言語とPython言語の比較

出題に使われているプログラミング言語だけど、これは共通テスト手順記述言語(DNCL)というものなんだ。

はるのど。初めて見る言語だったので、戸惑ったけれど、前にPythonを学んだので、何となく理解できました。

それはよかった。じゃあ、同じ処理を行うPythonプログラムを作ってみたので、比較してみよう。
DNCL言語とPython言語の比較
| No | DNCL | Python | コメント |
|---|---|---|---|
| 01 | Tomei = [“A党”,”B党”,”C党”,”D党”] | Tomei = [“A党”, “B党”, “C党”, “D党”] | 政党名をリスト定義 |
| 02 | Tokuhyo = [1200, 660, 1440, 180] | Tokuhyo = [1200, 660, 1440, 180] | 得票数をリスト初期化 |
| 03 | sousuu = 0 | sousuu = 0 | 合計得票数を格納する変数を初期化 |
| 04 | giseki = 6 | giseki = 6 | 議席数を格納する変数を定義 |
| 05 | mを0から ア まで1ずつ増やしながら繰り返す; | for m in range(len(Tokuhyo)): | 各得票数を合計するための繰り返し |
| 06 | L sousuu = sousuu + Tokuhyo [m] | sousuu += Tokuhyo[m] | 得票数を総得票数に加算 |
| 07 | kizyunsuu = sousuu / giseki | kizyunsuu = sousuu / giseki | 基準得票数を議席数で割って算出 |
| 08 | 表示する(“基準得票数:”,kizyunsuu ) | print(“基準得票数:”, kizyunsuu) | 基準得票数を画面に出力 |
| 09 | 表示する(“比例配分”) | print(“比例配分”) | 比例配分結果を出力開始 |
| 10 | mを0から 3 まで1ずつ増やしながら繰り返す: | for m in range(4): | 0から3まで繰り返し処理 |
| 11 | L表示する (Tomei [m], “:”, Tokuhyo/kizyunsuu) | print(Tomei[m], “:”, Tokuhyo[m] / kizyunsuu)? | 政党ごとの得票割合を出力 |
Pythonコードによる実行
# 政党の名前リスト
Tomei = ["A党", "B党", "C党", "D党"]
# 各政党の得票数リスト
Tokuhyo = [1200, 660, 1440, 180]
# 総得票数を初期化
sousuu = 0
# 議席数
giseki = 6
# 得票数の合計を計算
for m in range(len(Tokuhyo)):
sousuu += Tokuhyo[m]
# 基準得票数を計算
kizyunsuu = sousuu / giseki
print("基準得票数:", kizyunsuu)
# 比例配分の結果を表示
print("比例配分")
for m in range(4):
print(Tomei[m], ":", Tokuhyo[m] / kizyunsuu)
では今回のPythonプログラムを実際に実行してみよう。Google Colabによる実行例はこちらを実行してみて
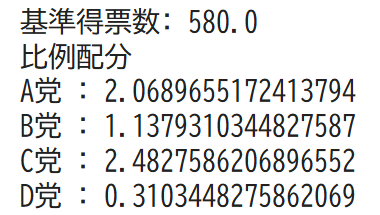

図4と同じ結果が出たね。

プログラムの正しさを確認できたね。こうして実際に、実際に動かしてみると、より深い理解につながるよ。Google Colabでパラメータを変えたりして、試してみてね。
- 変数の命名規則
変数は英字で始まる英数字とアンダースコアを使用できる。小文字は通常の変数、大文字は配列、全て大文字は定数を表す。 - 表示文
数値や文字列、変数の値を「~を表示する」として出力する。複数の値を表示する場合は「と」で区切って並べる。 - 代入と演算
値の代入は「←」を使い、算術演算(+,-,*,/)、比較演算(=,≠,>,<)、論理演算(かつ、または、でない)が利用できる。 - 制御構文
条件分岐文や繰り返し文を用いて処理の流れを制御する。条件分岐では「もし~ならば~を実行する」を使い、繰り返しには条件繰返し文や順次繰返し文がある。 - 関数の定義と利用
DNCLには用意された関数を呼び出すことが可能で、新しい関数を定義することもできる。関数の定義は「関数~を~と定義する」と表現する。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジ!
編集者ひとこと
いよいよプログラミング問題です。ここで使われているDNCL言語は受験生の取り組んでいたプログラミング言語によって有利・不利になるとして、大学入試センターが用意したそうです。DCNLは、「Daigaku Nyushi Center Language」の略と噂されていますが、ローマ字というところがなんとも言えないセンスですね・・。
プログラミングの問題ですが、正確に解答するには問題の読解能力が必要。穴埋め問題ですが、問題の意味が理解できないと悩んでしまうかもしれません。問2以降はさらに、複雑になるので、何とかついてきてくださいね。
<RANKING>![]()
高校教育ランキング



