問題
問題文
| 出典:独立行政法人大学入試センター 公開問題「平成30 年告示高等学校学習指導要領に対応した令和7年度大学入学共通テストからの出題教科・科目 情報サンプル問題」 https://www.mext.go.jp/content/20211014-mxt_daigakuc02-000018441_9.pdf |
次の文章の空欄(エ)~ (ス)に入れる最も適当なものを、後の解答群のうちから一つずつ選べ。同じものを繰り返し選んでもよい。
M さん: 先生、比例代表選挙では各政党の当選者数はどうやって決まるのですか? 当選者数が整数なので、割合だけだと上手くいかなかったのです。
先 生: 様々な方法があるけど、日本では各政党の得票数を1、2、3、… と整数で割った商の大きい順に定められた議席を配分していく方法を採用しているよ。この例だと表2のように(1)から(6)の順に議席が各政党に割り当てられるんだ。C党が(1)の議席を取っているけど、このとき、何の数値を比較したか分かるかな。
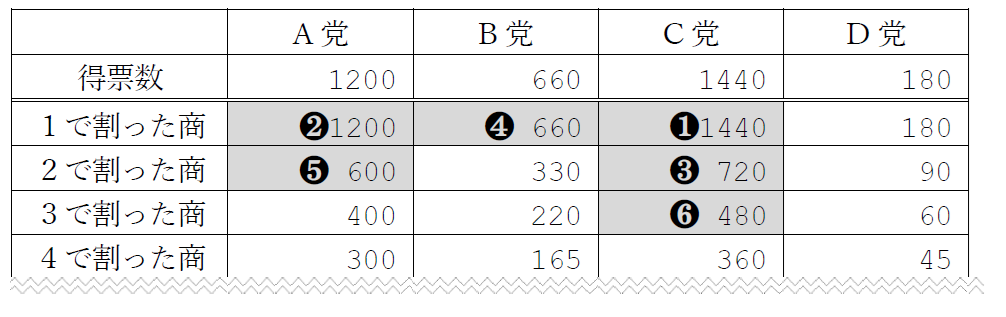
Mさん:1で割った商です。A党から順に1200,660,1440,180 ですね。
先 生:そうだね。ではA党が(2)の議席を取るとき,何の数値を比較したのだろうか。
Mさん:C党は1議席目を取ったので,1440 を2で割った商である720 を比較します。A党から順に1200,660,720,180 ですね。この中で数値が大きいA党が議席を取ります。なるほど,妥当な方法ですね。
Kさん:この考え方で手順を考えてみようよ。
先 生:まずは候補者が十分足りるという条件で手順を考えてみるのがいいですよ。
Kさん:各政党に割り当てる議席を決めるために,比較する数値を格納する配列Hikaku がいるね。
Mさん:各政党に配分する議席数(当選者数)を格納する配列Tosen も必要だね。最初は議席の配分が行われていないから,初期値は全部 0 にしておくね。


Kさん:「2 で割った商」の「2」のように、各政党の得票数を割るときに使う数字はどうすればいいかな。
Mさん: その政党の当選者数+1でいいよね。配列Tosenが使えるね。そうだ、変化したところだけ計算し直せばいいんじゃない? 議席を配分する手順を書いてみよう。
| 手順1 | 配列Tokuhyo の各要素の値を配列Hikaku の初期値として格納する |
| 手順2 | 配列Hikaku の要素の中で最大の値を調べ,その添字maxi に対応する配列Tosen[maxi]に1 を加える。 |
| 手順3 | Tokuhyo[maxi]をTosen[maxi]+1 で割った商をHikaku[maxi]に格納する。 |
| 手順4 | 手順2と手順3を当選者数の合計が議席数の6になるまで繰り返す。 |
| 手順5 | 各政党の党名(配列Tomei)とその当選者数(配列Tosen)を順に表示する。 |
Kさん: この図7の手順が正しいか確認するために、配列Hikakuと配列Tosenの中がどう変化していくか確認してみよう。図8 のようになるね。
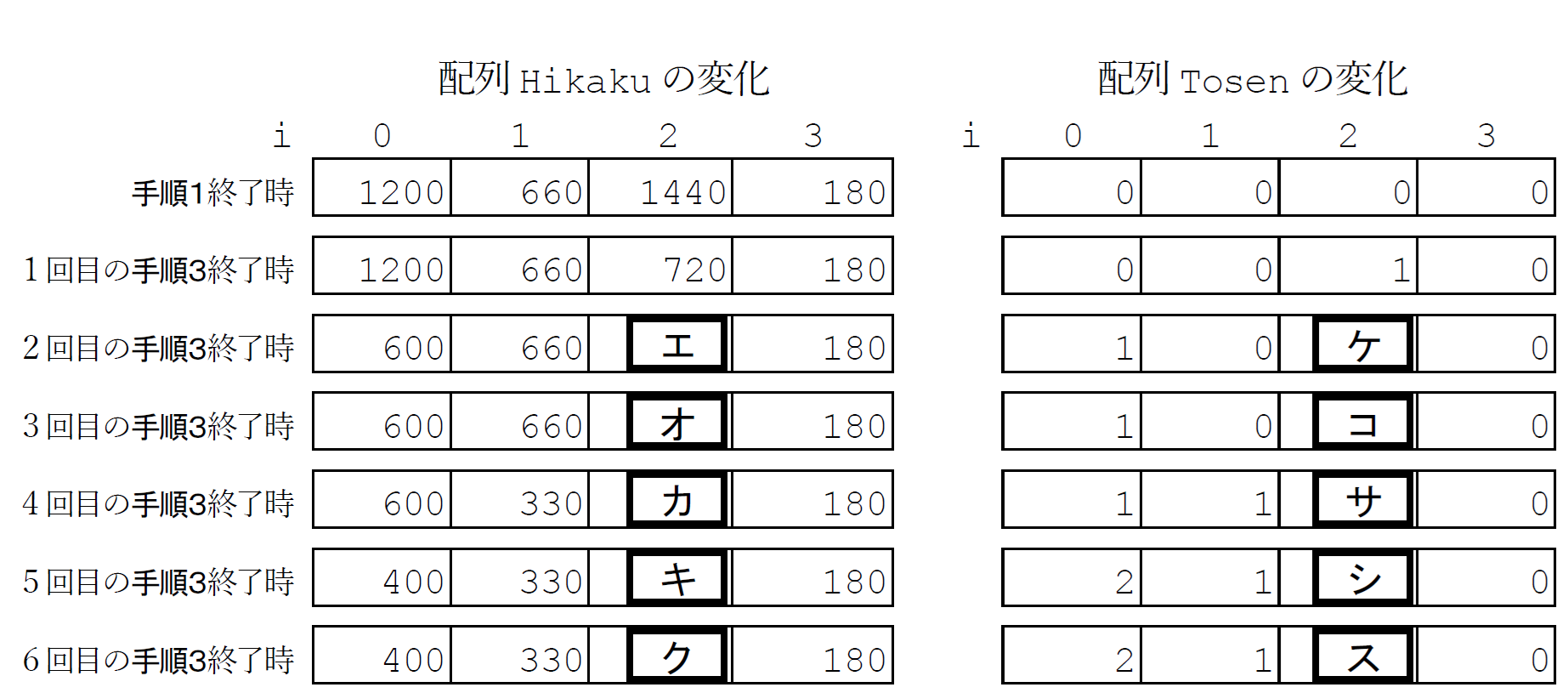
Mさん: 先生に教えてもらった結果と同じように、議席数が6になるまで議席を配分できたね。この手順でプログラムを考えてみよう。
解答群
解答
- (エ)(b)720 、(ケ)(1) 1
- (オ)(9)480 、(コ)(2) 2
- (カ)(9)480 、(サ)(2) 2
- (キ)(9)480 、(シ)(2) 2
- (ク)(7)360 、(ス)(3) 1
解説
比例代表選挙における当選者数を決めるプログラムの開発にチャレンジします。問1で検討したプログラムでは、小数点以下の処理に問題があったことから、「ドント式」という日本の国政選挙でも利用されている議席割り当て方式を用います。最初にドント式の仕様を定義し、次にこの仕様を実現するための設計を行い、設計の正しさを確認するという一連の流れを、問題を解きながら体験しましょう。
黒板
ドント方式とは?

問1では得票数に比例した、政党ごとの当選者数を求めるプログラムを作ったけれど、少数の扱いで問題が発生したよね。

どうやっても、当選者数が議席数と合わせる事が出来なくて、困りました。これでは、議員の数が合わなくなってしまう、もっと良いやり方があるはずですが・・・。

それは困ったね。実は、日本の比例代表選挙では、「ドント式」という議席の配分方式が使われているんだ。

ドント式?。そんな方式があるのなら、最初から知りたかった。

ドント式は、各政党の総得票数をそれぞれ1,2,3,4・・・と自然数で割っていき、得られた商の大きい順に議席を配分する方式だよ。
開発プロセス

問題の中では、「表2」を使って、ドント方式の仕様を説明しているよね。このようにプログラムの仕様を決めることを「要件定義」というんだ。

要件定義ですか?じゃあ、そのあとで配列を定義したり、処理の手順を決めたりするのは、なんというのですか?

これは「設計」だね。大きなシステムでは「基本設計」、「詳細設計」というように段階的に細かくしていくよ。

なるほど設計ですか。でも設計しただけではコンピュータでは動かないですよね。

そうだね。設計の後の「実装」という工程で、実際にプログラミングをするんだ。

やっと、プログラミングができるんですね。

ちょっと待ってね。プログラミングの前に、設計の正しさを確認するために、手順を紙の上でトレースしてみよう。

トレース?そんな面倒なことをせずに、プログラミングじゃダメなんですか?

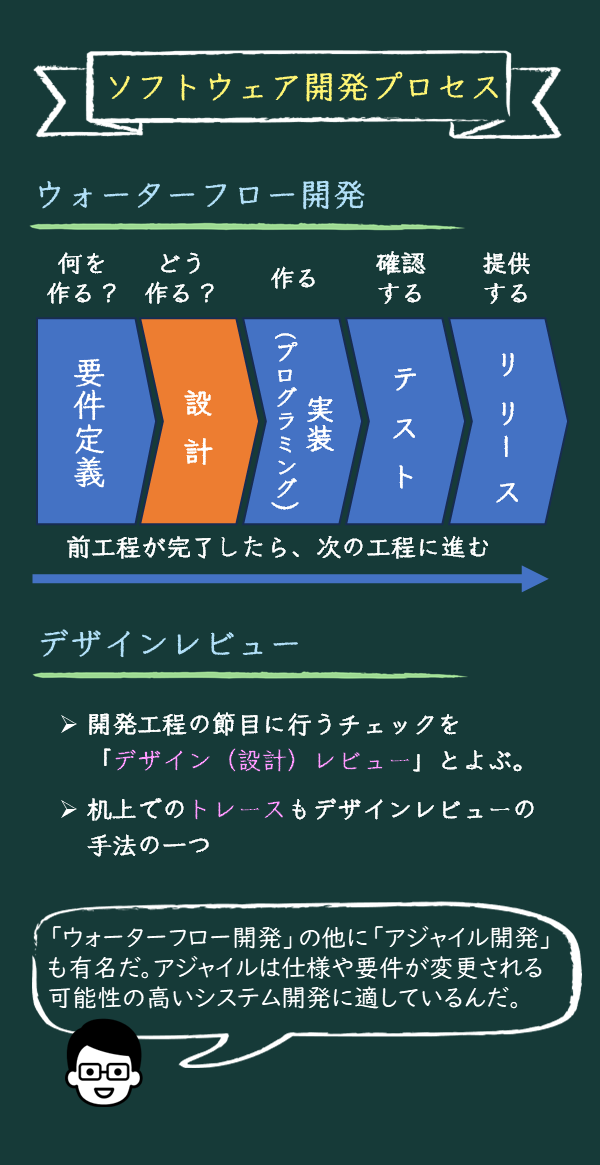
まあ、そう焦らずに。開発手法にもいろいろあるけれど、今回は「ウォーターフォール型」で進めよう。ウォーターフォールとは滝の事で、滝のように上から下へ、つまり上流工程から下流工程へと順番に開発が進められていく開発手法なんだ。

うーん、滝のなかで溺れないよう、じっくりやります。
手順1 配列Hikakuの初期化

さあ、図7の手順1から順番に行くよ。手順1は「配列Tokuhyo の各要素の値を配列Hikaku の初期値として格納する」だ。つまり、値をコピーすればよいよ。

そのままコピーするだけなら、簡単です。ところで、配列Tokuhyo、配列Hikakuは何を意味しているんでしょうか?

Hikakuは「各政党の得票数と整数で割った商」が入る配列で、Tosenは当選者数を格納する配列だよ。

なるほど、つまり表2がHikaku配列の変化を示しているということですね。

その通り。まずトレースの第一のコツは、「初期状態をしっかり把握する」だ。
手順2 配列Hikakuから、当選者数を求める
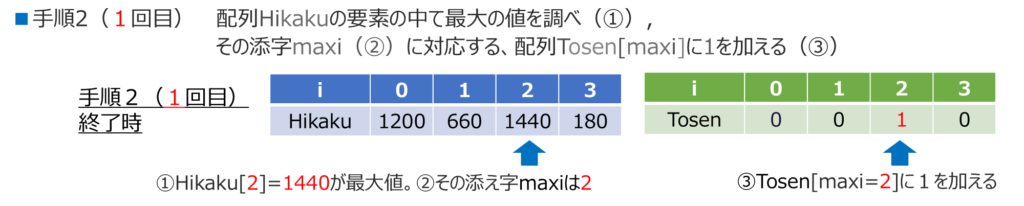

手順2は「 配列Hikaku の要素の中で最大の値を調べ,その添字maxi に対応する配列Tosen[maxi]に1 を加える。」だ

添え字maxiってなんですか?

添え字とは、配列の各要素に割り振られた番号だよ。各配列の「i」が該当するんだ。ここでは、最大値の添え字「i」という意味なので、「maxi(マックスアイ)」と命名されているんだ。

なるほど。Hikakuの中で最大なのは、Hikaku[2]の1440だね。だから添え字maxiは2ですね。

その通り!じゃあ、その添字maxi に対応する配列Tosen[2]に1 を加えてみよう。

最初はTosenは全部0だから、Tosen[2]に1を加えては1になります。

?いいね。このように、1ステップずつ丁寧に進めることが、トレースには重要だね。
手順3 当選者を除いて、Hikaku配列を更新する


手順3は「Tokuhyo[maxi]をTosen[maxi]+1 で割った商をHikaku[maxi]に格納する。」だね。まずはTosen[maxi]+1を計算してみて。

はい。maxiは2だから、Tosen[maxi]というのはTosen[2]の事ですね。Tosen[2]の値は1だから、Tosen[maxi]+1=2になります。

さすが、ちゃんと変数の変化をつかめているね。Tokuhyo[maxi]は1440だから、今求めた2で割ると720となるね。この720をHikaku[2]に新しく格納するんだ。

Hikaku = [1200, 660, 720, 180]になりますね。

その通り!手順3のポイントは、変数の変化を常に追跡するだね。HikakuやTosenの配列を書き出して、新しい値に更新していこう。
手順4 当選者数が6になるまで繰り返し


ここから同じ処理を繰り返していくよ。当選者の合計が6になるまで、手順2と手順3を繰り返すんだ。

あとはひたすら繰り返すんですね。判定処理などの繰り返し条件を見逃さないように、しっかりトレースします。

いいね。じゃあ私が手順2を計算するから、なおや君は手順3と手順4の判定をやってね。
2回目の繰り返し処理(手順2,3)
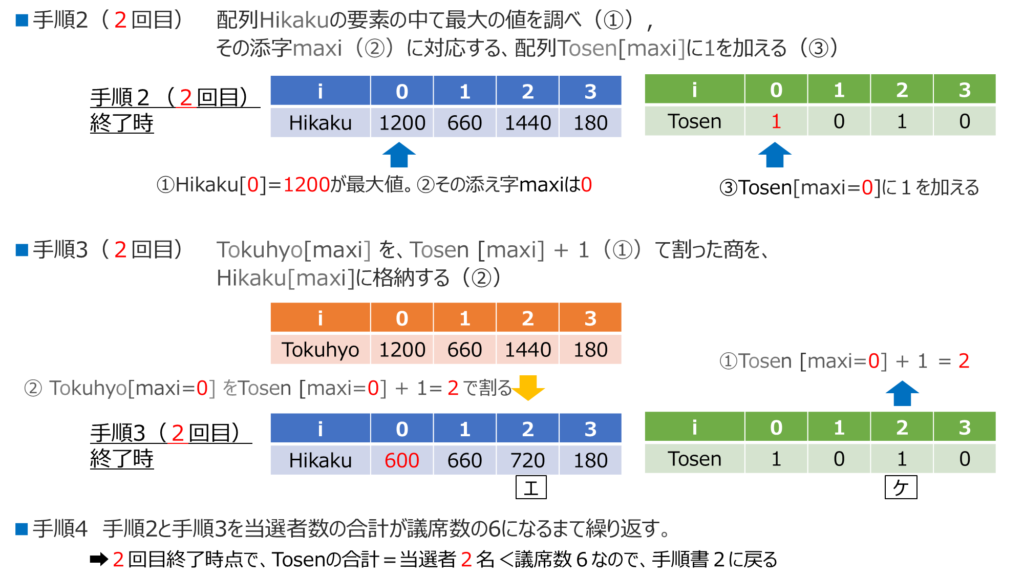

手順2で、Hikaku[0]=1200が最大値だから、Tosen[0]に1を加えて1にする。

手順3で、Hikaku[0]の1200を、Tosen[0]+1=2で割った 600をHikaku[0]に格納すればよいですね。そして当選者は2名なので、手順2に戻るですね。慣れてきました。
3回目の繰り返し処理(手順2,3)


手順2で、Hikaku[2]=720が最大値だから、Tosen[2]に1を加えて2にする。

手順3で、Hikaku[2]の720を、Tosen[2]+1=3で割った 480をHikaku[0]に格納します。まだ当選者は3名なので、手順2に戻ります。
4回目の繰り返し処理(手順2,3)


手順2で、Hikaku[1]=660が最大値だから、Tosen[1]に1を加えて1にする。

手順3で、Hikaku[1]の660を、Tosen[1]+1=2で割った 330をHikaku[1]に格納します。当選者は4名なので、手順2に戻ります。
5回目の繰り返し処理(手順2,3)


手順2で、Hikaku[0]=600が最大値だから、Tosen[0]に1を加えて1にする。

手順3で、Hikaku[0]の600を、Tosen[0]+1=3で割った 400をHikaku[1]に格納します。当選者は5名なので、手順2に戻ります。
6回目の繰り返し処理(手順2,3)


手順2で、Hikaku[2]=480が最大値だから、Tosen[2]に3を加えて1にする。

手順3で、Hikaku[2]の480を、Tosen[2]+1=4で割った 360をHikaku[2]に格納します。ついに当選者6名になったので、これで繰り返し終了です。
- ウォーターフォール開発の特徴
上流工程から下流工程へ順番に進む開発手法。各工程が完了してから次の工程に進むため、計画的な進行が求められる。 - 要件定義の重要性
1システムやプログラムが満たすべき機能や動作を定義する工程。正確な要件定義が、成功する開発の基盤となる。 - 基本設計と詳細設計
基本設計ではシステム全体の概要を決定し、詳細設計では各処理の具体的な手順やデータ構造を設計する。 - デザインレビューの役割
開発工程の節目に行う設計の確認プロセス。設計が正確であるか、仕様通りに進んでいるかを確認し、品質を確保する。 - トレース時のポイント
初期状態の確認、ステップごとの変化、繰り返し処理の追跡、最大値の確認、最終結果の検証が重要。これにより設計が正しく実行されているか確認できる。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジ!
編集者ひとこと
いよいよ本格的なアルゴリズムの問題です。プログラムを作る為の要件定義から、設計までを、丁寧に説明しています。
しっかりプログラムをトレースするには、結構根気がいるので、丁寧にステップ毎に追っていくことが必要となります。
ちょうど今、衆議院選が始まったところで、ニュースで「ドント方式」の説明がされていました。思わず、「プログラミングできるよ!」と言いたくなりましたね。
<RANKING>![]()
高校教育ランキング



