この授業では、散布図と相関係数を使って2つの変量間の関係を学び、回帰直線を描いてデータの傾向を視覚的に把握する方法を学びます。また、データ分析の応用についても考えます。
黒板
授業

2つの変量の関係ってどういうこと?

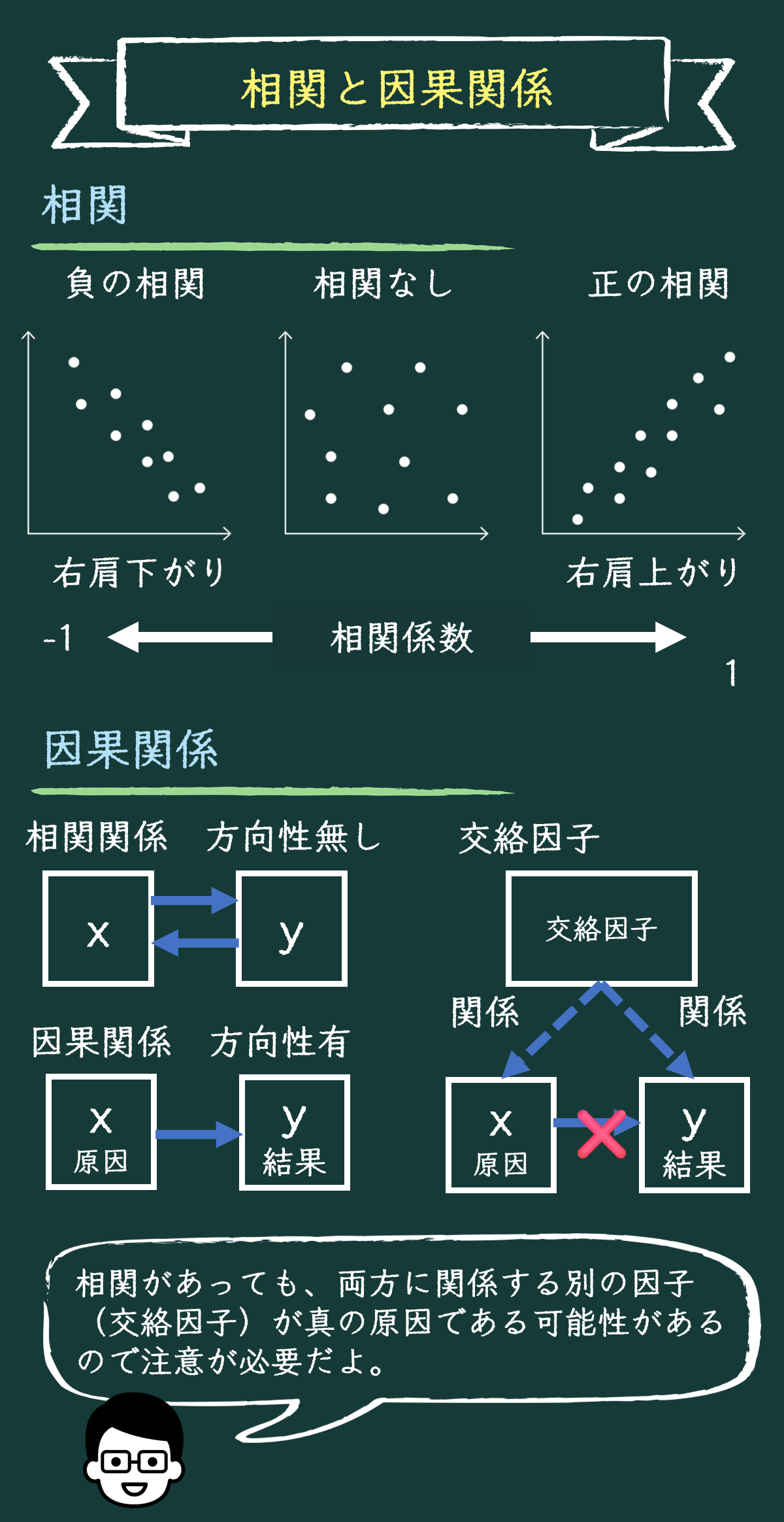
例えば一方の変量が増加すると他方も増加する傾向が見られるときには、「正の相関」があると言える。逆に、一方が増加すると他方が減少する傾向が見られるときには、「負の相関」があるんだ。そして、どちらの傾向も見られないときは、「相関がない」と判断するんだよ。

例えば、勉強をすると、テスト成績が良くなるというのは正の相関ですか?

その通りだね!勉強時間とテストの点数には正の相関がありそうだね。じゃあ、負の相関にはどんなものがあるだろう?

運動する時間が増えると、体重が減るというのはどうですか?

いいね。相関の強さを示す際に、相関係数で表すことができるよ。相関係数は、+1に近いほど強い正の相関を示し、-1に近いほど強い負の相関を示すんだ。

なるほど、数値で示すことで、誰が見ても結果が明らかになりますね。原因と結果の関係といってよいですか?

良い質問だね。原因から結果へのつながりがある関係のことを因果関係というけれど、相関があっても因果関係はないという場合もあるよ。

どういうこと?

データをとったら身長と計算能力に相関関係があったらこれも因果関係があると言えるかな?

うーん、そんなことはないと思うけれど。実は、いろんな学年の生徒が混ざっているデータなんじゃない?

鋭いね、正解です。このデータのように、両方に関係する別の因子(交絡因子)が真の原因である可能性があるので注意が必要だ。このケースでは「学年」がそれにあたるよ。

なるほど!相関を見つけても、ちゃんと背景や他の要因も考えないといけないんですね。
アヤメデータを用いたデータ分析

じゃあ、これから実際のデータを用いたデータ分析を行おう。利用するデータは、「irisデータセット」という、アヤメの花びらのデータだよ。

アヤメの花びら?なんでそんなデータを使うの?

「irisデータセット」は、データサイエンスの世界では非常に有名なんだ。1936年にイギリスの統計学者ロナルド・フィッシャーが発表したもので、データ分析や機械学習の教材として今でも広く使われているんだよ。

へぇ、そんな昔からあるんだ。それにしても、なんでこのデータセットがそんなに有名なんですか?

実は「irisデータセット」は、非常にシンプルで理解しやすい上に、データを分析するためのライブラリの中にデータが収録されているんだ。

ふーん。サンプルデータみたいな感じなんだね。
irisデータセットの内容
import seaborn as sns
# Irisデータセットを読み込み
iris = sns.load_dataset("iris")
# DataFrameを表示
iris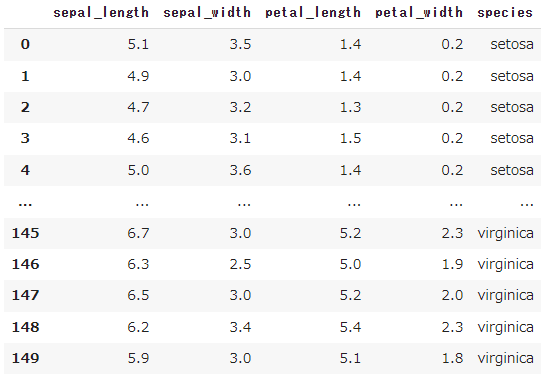

じゃあ、実際のデータを見てみよう。次のpythonコードをGoogle Colaboratoryに入力してみて。Google Colaboratoryについては、前回(45.データの整形と修正)詳しく解説しているので、初めての人はそちらから確認してね。

おお、表示された。150個のデータですね。Lengthとか、widthとかあるので、何かの大きさのデータですか?

その通り「花びらの長さ(Petal Length)」「花びらの幅(Petal Width)」「ガクの長さ(Sepal Length)」「ガクの幅(Sepal Width)」という4つの特徴量で構成されているんだ。

speciesというのはアヤメの種類のようですね。

そうだねこれは、3種類のアヤメの種類「setosa(セトーサ)」、「versicolor(ヴァーシカラー)」、「virginica(ヴァージニカ)」のことだ。

特徴量と分類

ところで、特徴量って、何かの特徴を表す数字ってことですか?

その通り。たとえば、花びらが長くて幅も広いと「Virginica」かもしれないし、逆に短くて細いと「Setosa」かもしれないっていう具合だね。今日は特徴量を使って、どの花がどの種類なのかを見分けていくよ。

花の種類を特徴別に分類するということですね。
散布図・相関行列グラフの表示
# Irisデータ 散布図・相関行列
import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
# Irisデータセットを読み込む
iris = sns.load_dataset("iris")
# ペアグリッドを作成し、種ごとに色分け
g = sns.PairGrid(iris, hue="species")
# 下三角部分に相関係数を表示
def corrfunc(x, y, **kws):
species = iris['species'].unique() # 種を取得
corr_values = {}
for sp in species:
data = iris[iris['species'] == sp] # 特定の種のデータを取得
# 相関係数を計算
r = np.corrcoef(data[x.name], data[y.name])[0, 1]
corr_values[sp] = r # 計算した相関係数を保存
ax = plt.gca() # 現在の軸を取得
# 各種の相関係数をグラフ内に表示
ax.annotate(f'Setosa: ρ = {corr_values["setosa"]:.2f}\n'
f'Versicolor: ρ = {corr_values["versicolor"]:.2f}\n'
f'Virginica: ρ = {corr_values["virginica"]:.2f}',
xy=(0.5, 0.5), xycoords='axes fraction',
ha='center', va='center',
fontsize=10, bbox=dict(facecolor='white', edgecolor='none', pad=2.0))
# 下三角部分に相関係数を表示
g.map_lower(corrfunc)
# 上三角部分に散布図を表示
g.map_upper(sns.scatterplot)
# 対角線にヒストグラムを表示
g.map_diag(sns.histplot)
# 凡例を追加
g.add_legend()
# グラフを表示
plt.show()

じゃあ、Google Colaboratoryを使ってグラフを作ってみよう。

はい、もう慣れてきました。Pythonのプログラムコードを実行してみます。おっ!表の中にグラフが表示されていて複雑なグラフですね。

特徴量の間の関係を行列で表しているんだね。

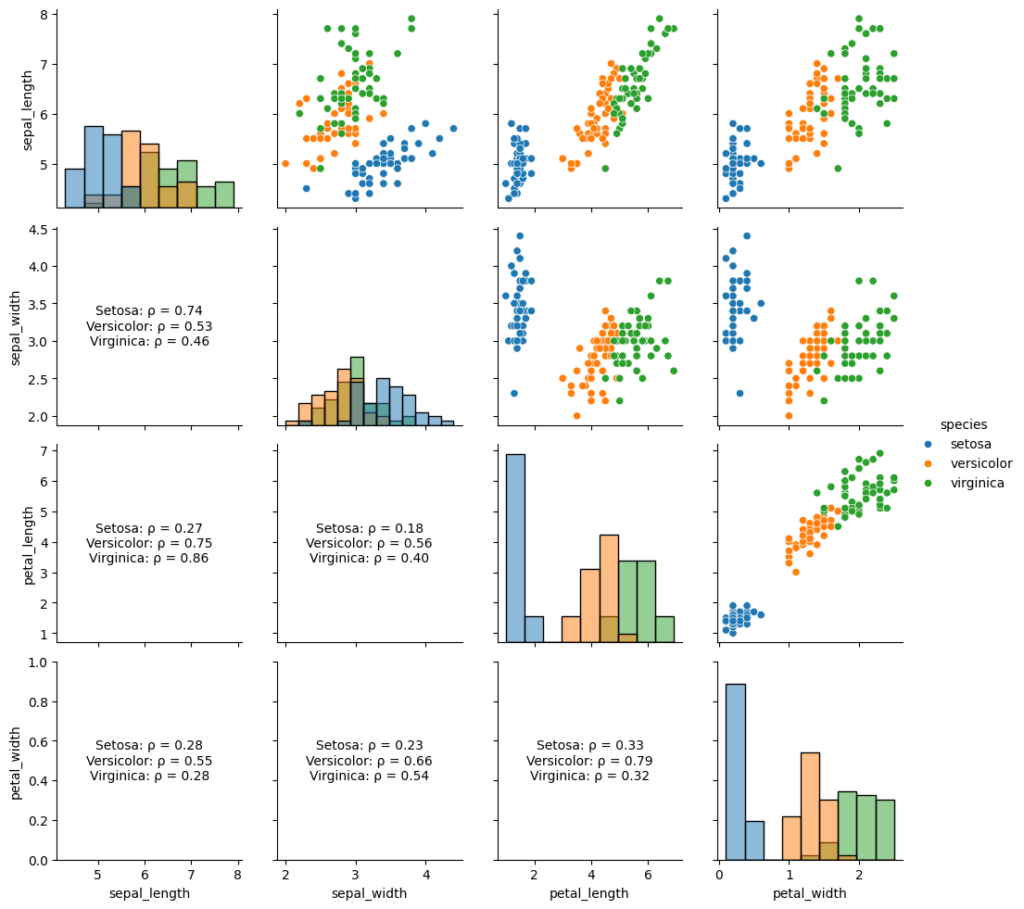
その通り。まずはヒストグラムを見てみよう、Setosaの花びらの長さ(Petal Length)に注目してみて。上から3行目、左から3列目のグラフだよ
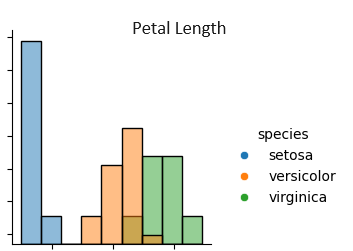

Setosaの花びらの長さ(Petal Length)って、全部同じような長さで、他の種類とは明らかに違いますね。

そうだね。Setosaは、花びらの長さ(Petal Length)が他の2つの種類よりも明らかに短くて、その分布も非常に狭い範囲に集中しているんだ。これがSetosaの特徴だね。

なるほど、それだけでSetosaかどうかがわかりそうですね。他の変数でも同じように特徴があるんですか?

そうだね。ガクの幅(Sepal Width)についても同じように、Setosaは他の種類よりも幅広いんだ。これもSetosaを見分けるポイントになるよ。
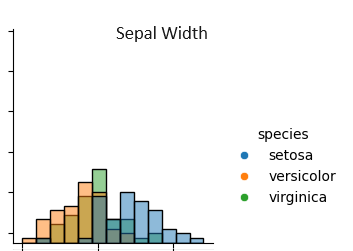

上から2行目、左から2列目のグラフですね。なるほど、ヒストグラムを見るだけで特徴がわかってきますね!
散布図から見える関係

次に、散布図を見てみよう。散布図は、2つの変数間の関係を視覚的に表すためのグラフだよ。例えば、花びらの長さ(Petal Length)と幅(Petal Width)の関係を見てみようか。上から3行目、一番右のグラフだよ。
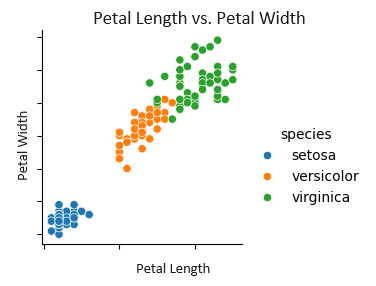

Setosaはやっぱり他の2つとは違って、全然違う場所に固まっていますね。花びらの長さ(Petal Length)も幅(Petal Width)も短くて狭い感じがします。

その通り。Setosaははっきりと分かれていて、VersicolorとVirginicaはもっと重なり合っているんだ。これは、花の種類を見分けるために役立つ重要な情報だよ。

じゃあ、VersicolorとVirginicaの区別はちょっと難しそうですね…
相関関係からの洞察

さて、次は相関関係を見ていこう。Virginicaの花びらの長さ(Petal Length)と幅(Petal Width)の相関係数を見て。1番下で、3列目の箱だよ。
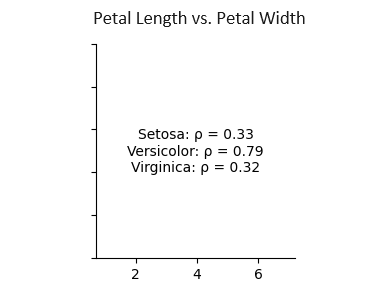

Setosaは0.33、Versicolorは0.79、Virginicaは0.32だね。Versicolorだけが、強い相関があるようですね。

さて、ここまで見てきた結果をまとめてみようか。それぞれの種類のアヤメには独自の特徴があることがわかったね。Setosaは特にわかりやすい例で、花びらの長さ(Petal Length)やガクの幅(Sepal Width)から他の種類と簡単に区別できるんだ。

はい、Setosaは簡単に見分けられますね。でも、VersicolorとVirginicaは少し難しかったです。

そうだね。でも、複数の変数を組み合わせて見ていくことで、その違いを明確にすることができるんだよ。これがデータ分析の醍醐味だね。いくつもの視点からデータを見ることで、新しい発見が生まれるんだ。

うん、なんかデータをいろいろな角度から見ることが大切だってことがわかりました。もっと色んなデータで試してみたいな!
回帰式の作成
# Irisデータ 花びらの長さ(Petal Length)と幅(Petal Width)の回帰直線
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
# Load the iris dataset
iris = sns.load_dataset("iris") # Seabornからirisデータセットをロード
# 関数を作成し、回帰直線、回帰式、相関係数をプロットする
def plot_regression_with_equation_and_correlation(x, y, data, species, ax, position):
sns.regplot(x=x, y=y, data=data, ax=ax, scatter=False, color="blue") # 回帰直線をプロット(散布図は表示しない)
ax.scatter(data[x], data[y], label=species, s=30) # 各種のデータ点をプロット
# 線形回帰モデルをフィットさせる
model = LinearRegression()
model.fit(data[[x]], data[y]) # 回帰モデルをデータに適用
intercept = model.intercept_ # 切片を取得
slope = model.coef_[0] # 傾きを取得
# 回帰直線の値を計算
x_vals = np.array(ax.get_xlim()) # x軸の範囲を取得
y_vals = intercept + slope * x_vals # y軸の値を計算して直線を描画
ax.plot(x_vals, y_vals, '--', color="red") # 回帰直線をプロット(破線で表示)
# 相関係数を計算
correlation = np.corrcoef(data[x], data[y])[0, 1]
# 回帰式と相関係数(ρ)を指定された位置に表示し、重ならないようにする
equation = f"{species}: y = {slope:.2f}x + {intercept:.2f}, ρ = {correlation:.2f}"
ax.text(position[0], position[1], equation, transform=ax.transAxes, fontsize=12, verticalalignment='top')
# matplotlibのfigureをセットアップ
fig, ax = plt.subplots(figsize=(12, 8)) # 12x8インチの図を作成
# 回帰式と相関係数を表示するための位置を定義
positions = [(0.05, 0.95), (0.05, 0.85), (0.05, 0.75)]
# 各種の回帰直線、回帰式、相関係数をプロット
for i, species in enumerate(iris['species'].unique()): # 各種ごとに処理
species_data = iris[iris['species'] == species] # 特定の種のデータを取得
plot_regression_with_equation_and_correlation("petal_length", "petal_width", species_data, species, ax, positions[i])
# 軸ラベルとタイトルを設定
ax.set_xlabel("Petal Length (cm)") # x軸ラベル
ax.set_ylabel("Petal Width (cm)") # y軸ラベル
ax.set_title("Petal Length vs. Petal Width with Regression Lines, Equations, and Correlations by Species") # グラフタイトル
# 凡例を追加
ax.legend(loc="best") # 最適な位置に凡例を表示
# グラフを表示
plt.show() # プロットを表示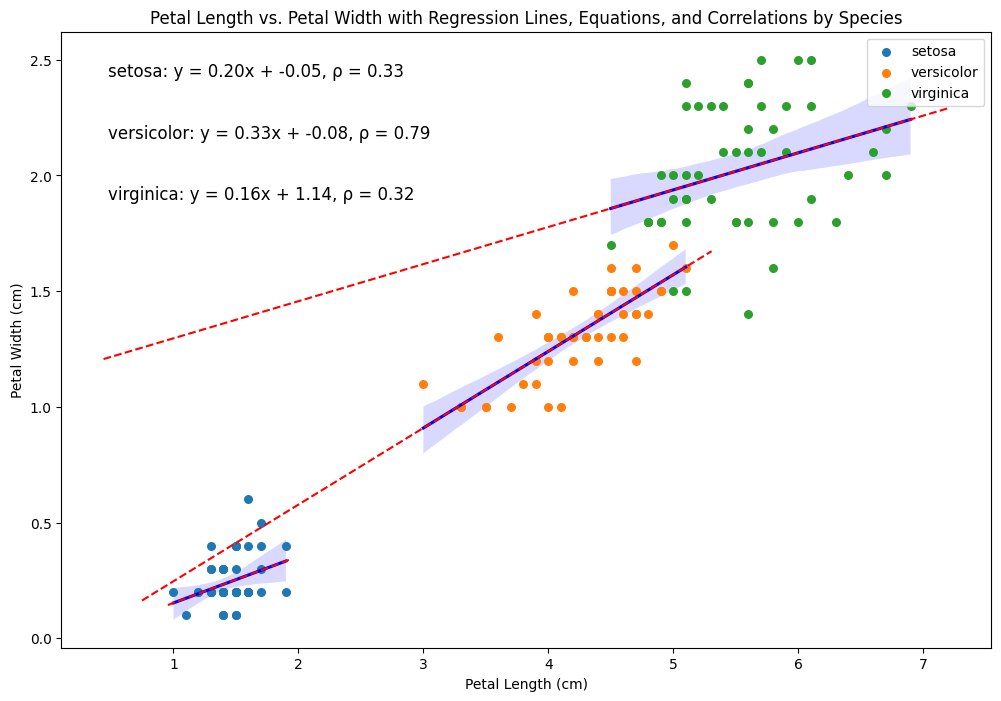

花びらの長さ(Petal Length)と幅(Petal Width)の関係をさらに詳しく見てみるために、回帰直線を描いてみよう。

回帰直線って何ですか?

回帰直線というのは、2つの変量の間にある関係を最もよく表す直線のことなんだ。たとえば、花びらの長さと幅のデータを散布図にプロットすると、その点のパターンに沿って最もよく当てはまる直線を引くことができる。この直線が回帰直線だよ。

なるほど、つまり、データがどの方向に進む傾向があるのかを見るための線なんですね。でも、どうやってその線を引くんですか?
回帰直線と回帰式

回帰直線を引くためには、まずデータの傾きを計算する必要があるんだ。傾きというのは、花びらの長さが1cm増えると、幅がどれくらい増えるかを示しているんだよ。そして、もう一つ大事なのが切片。これは、花びらの長さがゼロのときに幅がどれくらいになるかを示すんだ。

えっ、花びらの長さがゼロだと幅もゼロになるはずじゃないんですか?

そう思うよね。でも切片は、あくまで数学的な計算の結果なんだ。実際の花のサイズではなく、計算上の直線のスタート地点を示しているんだよ。だから、切片がマイナスの値になることもあるんだ。
アヤメの回帰直線

じゃあ、回帰直線もGoogle Colaboratoryを使って描いてみよう。次のpythonプログラムをノードブックに張り付けて実行してみて。

了解!散布図の上に直線が表示されて、数式も表示されました。

そうだね。表示された直線を回帰直線、数式を回帰式と呼ぶよ。

これをどう読み取ればよいんですか?

先生、Versicolorの回帰式って「Petal Width (y) = 0.33 × Petal Length (x) – 0.08」ですよね。この式を使うと、花びらの長さが増えると幅も増えることがわかるんですね。

そうだね、なおや君。この式によると、花びらの長さが1cm増えるごとに幅が0.33cm増えることになる。これは、花びらの長さと幅がそれなりに強い正の相関を持っていることを示しているんだ。

そうなんですね。回帰式を使うと、データの傾向が見えてきますね。他のアヤメの種類でも同じように分析してみたいです!

その好奇心は素晴らしいよ。次は他の種類の花びらについても同じように回帰式を使って分析してみよう。データの背後にあるパターンを発見することがデータ分析の醍醐味なんだよ。
データ分析の応用

その意欲が大事だよ、なおや君。データ分析は、実は日常生活の中でも多くの場面で役立つんだ。例えば、スポーツの成績を分析したり、SNSのトレンドを予測したり、ビジネスの戦略を立てたりするのにも使えるんだよ。

へぇ、そんなところでも使われているんですか。なんか、データ分析が急に身近に感じますね。

そうなんだ。だから、今日学んだことを基に、ぜひ色んなデータを自分で分析してみてほしいな。そうすることで、もっと深い理解が得られるはずだよ。

うん、これからもデータ分析を続けて、いろんなことを発見してみます!ありがとう、先生!
まとめ
名言解説
“To call in the statistician after the experiment is done may be no more than asking him to perform a post-mortem examination, he may be able to say what the experiment died of.”Ronald Fisher
この名言は、統計学の父と呼ばれるロナルド・フィッシャー(Ronald Fisher)の言葉です。フィッシャーは、20世紀を代表する統計学者であり、生物統計学の分野でも大きな貢献をしました。彼は特に実験デザインや仮説検定の方法論を発展させ、現代の統計学に多大な影響を与えました。
この名言の意味は、実験を行う前に統計学の視点を取り入れる重要性を強調しています。実験が終わってから統計学者を呼ぶのは、すでに実験が失敗した後でその原因を探るのと同じだということです。つまり、事前に統計的な計画を立てずに実験を進めてしまうと、結果が得られてもその信頼性や有効性が失われる可能性が高いという警告です。
データの収集方法や実験の条件を適切に設計することが大切です。統計学は、科学的な探求において重要な武器となります。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジ!
編集者ひとこと
今回の授業は、散布図・相関行列グラフという、かなりややこしいグラフを使っていたので、混乱したかもしれません。
しかし、大学入試センターが公開している”大学入学共通テスト「情報」サンプル問題 問題3”では、散布図・相関行列グラフと回帰直線を用いて、データ分析する問題が出題されています。グラフの見方がわからなければ答えられれない、かなりの難問です。
ということで、難しそうとあきらめず、実際にグラフをじっくり見て、自分で分析してくださいね。
<RANKING>![]()
高校教育ランキング



