サンプル問題２－３ プログラミング問題（比例選挙の議席数決定　その3)

問題

問題文

問３ 次の文章の空欄 セ ～ テ に入れる最も適当なものを，後の解答群のうちから一つずつ選べ。

Ｍさん：図９のプログラムを作ってみたよ。商を整数で求めるところは小数点以下を切り捨てる「切り捨て」という関数を使ったよ。

Ｋさん：実行したら図10 のように正しく政党名と当選者数が得られたね。

先生：できたようだね。各政党の当選者数は求められたけど，政党によっては候補者が足りない場合もあるから，その場合にも対応してみよう。図11 のように各政党の候補者数を格納する配列Kohoを追加してみたらどうだろう。例えば，Ｃ党の候補者が足りなくなるように設定してみよう。

Ｍさん：候補者が足りなくなったらどういう処理をすれば良いのですか？

先 生：比較した得票で次に大きい得票数の政党が繰り上がって議席を取るんだよ。

Ｍさん：なるほど。では，図９の(11)行目の条件文を次のように修正すればいいですね。当選していない候補者はどこかの政党には必ずいるという前提だけど。

Ｋさん：先生，候補者が不足するほかに，考えるべきことはありますか？

先 生：例えば，配列Hikakuの値が同じになった政党の数が残りの議席の数より多い場合，このプログラムでは添字の小さい政党に議席が割り当てられてしまうので不公平だね。実際には，この場合はくじ引きで議席を割り当てるようだよ。

解答群

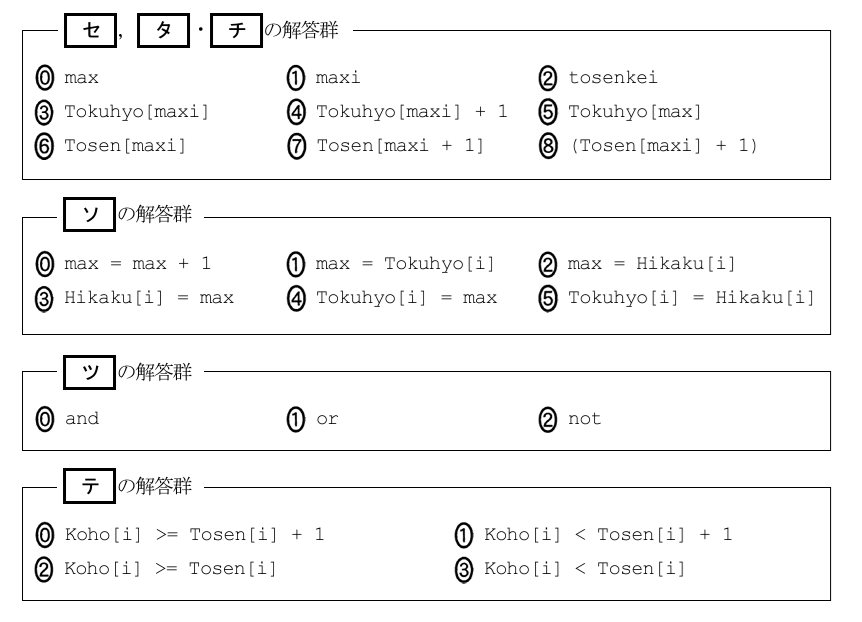
解答

解説

本日の授業では、問２で行った設計の手順に従ってプログラムを実装します。さらに、例外処理やログ出力を使って、プログラムの動きを可視化し、不正やエラーを防ぐための方法についても学びます

黒板

さて、いよいよプログラミングだ。この工程は「実装」あるいは「コーディング」ともいうよ。

待ってました。プログラムコードを作るから、コーディングというんですね。

そうだね。では、前問（２－２）でトレースした、図７の手順に従って進めよう。

はい。図７は最初見たときにはさっぱり意味が分かりませんでしたが、トレースして流れをつかんだので、ばっちりです。

手順1: 配列Tokuhyo の各要素の値を配列Hikaku の初期値として格納する

さて、（06）行の（ア）は２－１で回答済みだよね。何だったか覚えているかな？

えっと、（07)でTokuhyo の各要素の値を配列Hikaku にコピーするんだったよね。政党の数の４回分ループを回す必要があるから、要素は（ア）は3だね。

その通り！配列の要素が０から始まるということをちゃんと覚えていたね。さすが。

手順2: 配列Hikaku の要素の中で最大の値を調べ，その添字maxi に対応する配列Tosen[maxi]に1 を加える。

次は手順2を見てみよう。手順２を実装している部分はどこかわかるかな？

(11)の「もし max < Hikaku[i]ならば」のところが、最大値と比較してそうですね。

その通り。maxという変数はどういう役割をしているのかわかるかな？

多分、Hikaku[i]から読み取った数で一番大きい数として記録しているんじゃないでしょうか？

そうそう。そのためには、Hikaku[i]を読み込んで、maxの値を更新する必要があるよね。

わかった。（ソ）は「max = Hikaku[i]」でしょ。

正解。maxに代入されている値と配列の要素を比較して、配列の要素のほうが大きい場合値をmaxを上書きしているんだ。

そうか。(10）から(13)の処理で、maxiも決まったので、(14)の処理でTosen[maxi]に1を加えているんだね。

手順3: Tokuhyo[maxi]をTosen[maxi]＋1 で割った商をHikaku[maxi]に格納する。

次は（タ）と（チ）についてだね。これは手順3の一部であることが分かればすぐにわかるよね。

本当だ。（タ）はTokuhyo[maxi]で、（チ）はTosen[maxi]＋1 が入るね。

手順4: 手順２と手順３を当選者数の合計が議席数の６になるまで繰り返す。

当選者数の合計が議席数の6になるまでループを繰り返す必要があるから、ループカウンタ変数が必要だよね。

ループカウンタ変数って何？

プログラミングの繰り返し処理の回数を数える変数のことだよ。ループの中で、i =i +1というような変数があれば、iがループカウンタ変数だ。

じゃあ、(15)で出てくる、tosenkeiという変数があやしそうだね。

正解！。じゃあ、どこで手順４の「議席数の６になるまで」を判断しているだろう。

あっ！(08)の(セ)に「tosenkei 」が入るんじゃない？。これまで、（セ）が飛ばされてきたからおかしいと思った。

その通り。(08)から(16)の間は、tosenkei < gisekiが成り立つ間はループを続けるんだ。

最後の(17)から(18)は結果の表示だね。これで、穴埋めは完了！

例外処理の実装

ちょっと待って、まだ（ツ）、（テ）が残っているよ。これは候補者が足りなくなった場合の処理だ

得票があるのに、立候補していなんて政党はないでしょう？だから、考えなくてもいいんじゃないですか？

そういうわけにはいかないよ。予期せぬ事態や通常の処理ができなくなる状況に対処するたに、 「例外処理」を実装しておく必要があるよ。

えー、めんどくさい。

そういわずに、頑張ろう！ここでは先生が「比較した得票で次に大きい得票の政党が繰り上がって議席を取るんだよ。」と要件を定義しているよね。

繰り上がってと言われていも、どうやってプログラミングするのかわからないです。

じゃあ、今の手順を「その政党の投票が最大で、かつその政党の候補者が当選者より多ければ当選。候補者がいなければ、次の政党が当選」と言い換えたらどうだろう。

同じことを言っていますね。

じゃあ(11)「もし max < Hikaku[i] （ツ）、（テ）ならば」に今の日本語を当てはめてみて

(11)の前半部分が「もし max < Hikaku[i] 」の部分が、手順の「その政党の投票が最大で」のところまでを判断してますね。

その通り。では（ツ）（テ）は何だろう？

手順の「かつその政党の候補者が当選者より多ければ」ですね。（ツ）が手順の中の「かつ」のところですかね？選択肢を見ると「and」があるからこれがそれっぽいです。

正解！andは比較演算子といわれるもので、「かつ」を示すよ。

最後の（テ）には手順の「その政党の候補者が当選者より多ければ」に該当するから、「Koho[i] ＞＝ Tosen[i」」でいいんじゃないかな？

ファイナルアンサー？

えっ。違うの？

この場合、（14）行目で「Tosen[maxi] = Tosen[maxi] + 1」を行うことによって当選者数が候補者数を上回ってしまう可能性はないかな？

じゃあ、比較する際にあらかじめ当選者数に１加えておかないとだめということ？

その通り。だから（テ）に入るのは「Koho[i] ＞＝ Tosen[i」+1」になるよ。

うう、ムズイ！

そうだね。この後で、pythonでプログラミングしてみるから、そこでデバッグをしてみよう。

よろしくお願いします

Pythonコードによる実行

# 各政党の党名
Tomei = ["A党", "B党", "C党", "D党"]

# 各政党の得票数
Tokuhyo = [1200, 660, 1440, 180]

# 各政党の当選者数（初期化）
Tosen = [0, 0, 0, 0]

# 比較用の配列Hikaku
Hikaku = [0, 0, 0, 0]  # 初期化

# 議席数
giseki = 6

# 当選者の合計を表す変数
tosenkei = 0

# 配列の初期化（手順1:配列Tokuhyo の各要素の値を配列Hikaku の初期値として格納する）
for m in range(0, 4):  # (ア)の部分: 0から3までの4つの政党について処理する
    Hikaku[m] = Tokuhyo[m]

# 当選者数が議席数に達するまで繰り返す（手順4:手順2と手順3を当選者数の合計が議席数の6になるまで繰り返す）
while tosenkei < giseki:  # (セ)の部分: 議席数の6人に達するまで繰り返す
    max = 0
    maxi = 0

    # 最大値を探す（手順2:配列Hikaku の要素の中で最大の値を調べ，その添字maxi に対応する配列Tosen[maxi]に1を加える）
    for i in range(0, 4):  # アの部分: 0から3までの政党を調べ、最大の得票数を持つ政党を探す
        if max < Hikaku[i]:  # 最大値を探す
            max = Hikaku[i]
            maxi = i

    # 当選者を決定（最大得票の政党に議席を割り当てる）
    Tosen[maxi] += 1
    tosenkei += 1

    # 得票数を再計算（手順3:Tokuhyo[maxi]をTosen[maxi]＋1で割った商をHikaku[maxi]に格納する）
    Hikaku[maxi] = Tokuhyo[maxi] / (Tosen[maxi] + 1)  # (タ)と(チ)の部分: 新しい得票数を再計算

# 結果を表示（手順5:各政党の党名（配列Tomei）とその当選者数（配列Tosen）を順に表示する）
for k in range(0, 4):  # アの部分: 0から3まで、全政党の結果を表示する
    print(f"{Tomei[k]}: {Tosen[k]}名")

図９のDNCL言語のプログラムをPythonプログラムに変換したよ、実際に実行してみよう。Google Colabによる実行例はこちらを実行してみて。

図10と同じ結果が出たね。完璧だ！

5行目の得票数　Tokuhyo = [1200, 660, 1440, 180]　を変えると、結果がどう変化するか試してみてね。

Pythonコードによる実行（候補者が足りない場合）

# 各政党の党名
Tomei = ["A党", "B党", "C党", "D党"]

# 各政党の得票数
Tokuhyo = [1200, 660, 1440, 180]

# 各政党の当選者数（初期化）
Tosen = [0, 0, 0, 0]

# 各政党の候補者数
Koho =  [5, 4, 2, 3]  # A党は5人、B党は4人、C党は2人、D党は3人が候補者としている

# 比較用の配列Hikaku
Hikaku = [0, 0, 0, 0]  # 初期化

# 議席数
giseki = 6

# 当選者の合計を表す変数
tosenkei = 0

# 配列の初期化（手順1:配列Tokuhyo の各要素の値を配列Hikaku の初期値として格納する）
for m in range(0, 4):  # (ア)の部分: 0から3までの4つの政党について処理する
    Hikaku[m] = Tokuhyo[m]

# 当選者数が議席数に達するまで繰り返す（手順4:手順2と手順3を当選者数の合計が議席数の6になるまで繰り返す）
while tosenkei < giseki:  # (セ)の部分: 議席数の6人に達するまで繰り返す
    max = 0
    maxi = 0

    # 最大値を探す（手順2:配列Hikaku の要素の中で最大の値を調べ，その添字maxi に対応する配列Tosen[maxi]に1を加える）
    for i in range(0, 4):  # アの部分: 0から3までの政党を調べ、最大の得票数を持つ政党を探す
        # ツとテの部分: 最大得票数の条件と、候補者数が足りているかを確認する
        if max < Hikaku[i] and Koho[i] >= Tosen[i] + 1:  # (ツ)、(テ)の部分を追加
            max = Hikaku[i]
            maxi = i

    # 当選者を決定（最大得票の政党に議席を割り当てる）
    Tosen[maxi] += 1
    tosenkei += 1

    # 得票数を再計算（手順3:Tokuhyo[maxi]をTosen[maxi]＋1で割った商をHikaku[maxi]に格納する）
    Hikaku[maxi] = Tokuhyo[maxi] / (Tosen[maxi] + 1)  # (タ)と(チ)の部分: 新しい得票数を再計算

# 結果を表示（手順5:各政党の党名（配列Tomei）とその当選者数（配列Tosen）を順に表示する）
for k in range(0, 4):  # アの部分: 0から3まで、全政党の結果を表示する
    print(f"{Tomei[k]}: {Tosen[k]}名")

じゃあ、例外処理として、候補者が足りない場合のPythonプログラムも見てみよう。

11行目に候補者数　Koho = [5, 4, 2, 3]　の定義が追加されたのと、３４行目に（ツ）、（テ）の　and Koho[i] >= Tosen[i] + 1　が追加されたね。

結果はどうなった？Google Colabによる実行例はこちらを実行してみて。

C党の当選者が３から２に減って、A党の当選者が２から３に増えたね。C党は２名しか立候補していなかったから、しょうがないね。

候補者数が足りない場合の「例外処理」が正しくプログラミングできていることを確認できたね。

処理の見える化

先生、プログラムって勝手に処理してくれているじゃないですか？もう少し中で何が起こっているか見たいんですけど、どうすればいいんでしょうか？

いい指摘だね。「見えない部分」をちゃんと理解するためには、ログを出力することが必要なんだよ。

ログですか？それってエラーメッセージとか、そういうものですか？

エラーメッセージもログの一つなんだけど、それだけじゃないんだ。ログっていうのは、プログラムが処理している内容を、その都度表示して見える化するものなんだ。

具体的にはどんなものを表示させるの？

たとえば、プログラムの中でどの変数がどの値を持っているかとか、どの条件が満たされたかとか、そういったことを「ログ」として出力することで、プログラムがどう動いているのかが見えてくるんだよ。

ログの内容

でも、どんなログを出力すればいいんですか？プログラムが何か失敗した時にだけ出せばいいんじゃないですか？

もちろん、エラーが起きたときのログも重要だけど、それだけじゃ足りないよ。たとえば、今回の議席配分のプログラムを見てみよう。議席がどう割り振られていくのか、途中経過がわからないと、どこで何が起こっているか不明だよね。

確かに、結果だけじゃ途中でどういう処理がされたのかわかりませんね。

そうだよね。たとえば、配列HikakuやTosenがループごとにどう変化しているのか、ログで出力することで「この瞬間にはこの政党が最大の得票数を持っていたんだな」とか「今、議席が割り振られたんだな」っていうのが、追えるんだよ。

ログを使ったデバッグ

# 各政党の党名
Tomei = ["A党", "B党", "C党", "D党"]

# 各政党の得票数
Tokuhyo = [1200, 660, 1440, 180]

# 各政党の当選者数（初期化）
Tosen = [0, 0, 0, 0]

# 各政党の候補者数
Koho = [5, 4, 2, 3]  # A党は5人、B党は4人、C党は2人、D党は3人が候補者としている

# 比較用の配列Hikaku
Hikaku = [0, 0, 0, 0]  # 初期化

# 議席数
giseki = 6

# 当選者の合計を表す変数
tosenkei = 0

# ログを見やすくするためのセパレータ
separator = '-' * 40

# 配列の初期化（手順1:配列Tokuhyo の各要素の値を配列Hikaku の初期値として格納する）
for m in range(0, 4):  # (ア)の部分: 0から3までの4つの政党について処理する
    Hikaku[m] = Tokuhyo[m]

# 当選者数が議席数に達するまで繰り返す（手順4:手順2と手順3を当選者数の合計が議席数の6になるまで繰り返す）
while tosenkei < giseki:  # (セ)の部分: 議席数の6人に達するまで繰り返す
    max = 0
    maxi = 0

    # 各ループ開始時に配列の状態を表示
    print(f"{separator}")
    print(f"議席確定数: {tosenkei}/{giseki}")
    print(f"現在のHikaku = {Hikaku}")
    print(f"現在のTosen = {Tosen}")
    print(f"現在のKoho  = {Koho}")
    print("ループ開始。最大得票数を探します。")

    # 最大値を探す（手順2:配列Hikaku の要素の中で最大の値を調べ，その添字maxi に対応する配列Tosen[maxi]に1を加える）
    for i in range(0, 4):  # アの部分: 0から3までの政党を調べ、最大の得票数を持つ政党を探す
        print(f"  政党: {Tomei[i]}, 現在の最大値: {max}, Hikaku[{i}]={Hikaku[i]}, Koho[{i}]={Koho[i]}, Tosen[{i}]={Tosen[i]}")

        # ツとテの部分: 最大得票数の条件と、候補者数が足りているかを確認する
        if max < Hikaku[i] and Koho[i] >= Tosen[i] + 1:
            print(f"    条件成立: max < Hikaku[{i}] かつ Koho[{i}] >= Tosen[{i}] + 1")
            max = Hikaku[i]
            maxi = i
        else:
            print(f"    条件不成立")

    print(f"最大得票数を持つ政党: {Tomei[maxi]} (得票数={max})")

    # 当選者を決定（最大得票の政党に議席を割り当てる）
    Tosen[maxi] += 1
    tosenkei += 1

    # 得票数を再計算（手順3:Tokuhyo[maxi]をTosen[maxi]＋1で割った商をHikaku[maxi]に格納する）
    Hikaku[maxi] = Tokuhyo[maxi] / (Tosen[maxi] + 1)  # (タ)と(チ)の部分: 新しい得票数を再計算
    print(f"{Tomei[maxi]}の議席が増加。再計算後のHikaku[{maxi}] = {Hikaku[maxi]}")
    print(f"現在のTosen = {Tosen}")

# 結果を表示（手順5:各政党の党名（配列Tomei）とその当選者数（配列Tosen）を順に表示する）
print(f"{separator}\n最終結果:")
for k in range(0, 4):  # アの部分: 0から3まで、全政党の結果を表示する
    print(f"{Tomei[k]}: {Tosen[k]}名")

先ほどの各政党の当選者数を求めるプログラム に、ログを追加したよ。Google Colabによる実行例はこちらを実行してみて。

何かいっぱい、print文が追加されているね。ここでログを出力するんですね。では実行してみます。

ログ出力結果

----------------------------------------
議席確定数: 0/6
現在のHikaku = [1200, 660, 1440, 180]
現在のTosen = [0, 0, 0, 0]
現在のKoho  = [5, 4, 2, 3]
ループ開始。最大得票数を探します。
  政党: A党, 現在の最大値: 0, Hikaku[0]=1200, Koho[0]=5, Tosen[0]=0
    条件成立: max < Hikaku[0] かつ Koho[0] >= Tosen[0] + 1
  政党: B党, 現在の最大値: 1200, Hikaku[1]=660, Koho[1]=4, Tosen[1]=0
    条件不成立
  政党: C党, 現在の最大値: 1200, Hikaku[2]=1440, Koho[2]=2, Tosen[2]=0
    条件成立: max < Hikaku[2] かつ Koho[2] >= Tosen[2] + 1
  政党: D党, 現在の最大値: 1440, Hikaku[3]=180, Koho[3]=3, Tosen[3]=0
    条件不成立
最大得票数を持つ政党: C党 (得票数=1440)
C党の議席が増加。再計算後のHikaku[2] = 720.0
現在のTosen = [0, 0, 1, 0]
----------------------------------------
議席確定数: 1/6
現在のHikaku = [1200, 660, 720.0, 180]
現在のTosen = [0, 0, 1, 0]
現在のKoho  = [5, 4, 2, 3]
ループ開始。最大得票数を探します。
  政党: A党, 現在の最大値: 0, Hikaku[0]=1200, Koho[0]=5, Tosen[0]=0
    条件成立: max < Hikaku[0] かつ Koho[0] >= Tosen[0] + 1
  政党: B党, 現在の最大値: 1200, Hikaku[1]=660, Koho[1]=4, Tosen[1]=0
    条件不成立
  政党: C党, 現在の最大値: 1200, Hikaku[2]=720.0, Koho[2]=2, Tosen[2]=1
    条件不成立
  政党: D党, 現在の最大値: 1200, Hikaku[3]=180, Koho[3]=3, Tosen[3]=0
    条件不成立
最大得票数を持つ政党: A党 (得票数=1200)
A党の議席が増加。再計算後のHikaku[0] = 600.0
現在のTosen = [1, 0, 1, 0]
----------------------------------------
議席確定数: 2/6
現在のHikaku = [600.0, 660, 720.0, 180]
現在のTosen = [1, 0, 1, 0]
現在のKoho  = [5, 4, 2, 3]
ループ開始。最大得票数を探します。
  政党: A党, 現在の最大値: 0, Hikaku[0]=600.0, Koho[0]=5, Tosen[0]=1
    条件成立: max < Hikaku[0] かつ Koho[0] >= Tosen[0] + 1
  政党: B党, 現在の最大値: 600.0, Hikaku[1]=660, Koho[1]=4, Tosen[1]=0
    条件成立: max < Hikaku[1] かつ Koho[1] >= Tosen[1] + 1
  政党: C党, 現在の最大値: 660, Hikaku[2]=720.0, Koho[2]=2, Tosen[2]=1
    条件成立: max < Hikaku[2] かつ Koho[2] >= Tosen[2] + 1
  政党: D党, 現在の最大値: 720.0, Hikaku[3]=180, Koho[3]=3, Tosen[3]=0
    条件不成立
最大得票数を持つ政党: C党 (得票数=720.0)
C党の議席が増加。再計算後のHikaku[2] = 480.0
現在のTosen = [1, 0, 2, 0]
----------------------------------------
議席確定数: 3/6
現在のHikaku = [600.0, 660, 480.0, 180]
現在のTosen = [1, 0, 2, 0]
現在のKoho  = [5, 4, 2, 3]
ループ開始。最大得票数を探します。
  政党: A党, 現在の最大値: 0, Hikaku[0]=600.0, Koho[0]=5, Tosen[0]=1
    条件成立: max < Hikaku[0] かつ Koho[0] >= Tosen[0] + 1
  政党: B党, 現在の最大値: 600.0, Hikaku[1]=660, Koho[1]=4, Tosen[1]=0
    条件成立: max < Hikaku[1] かつ Koho[1] >= Tosen[1] + 1
  政党: C党, 現在の最大値: 660, Hikaku[2]=480.0, Koho[2]=2, Tosen[2]=2
    条件不成立
  政党: D党, 現在の最大値: 660, Hikaku[3]=180, Koho[3]=3, Tosen[3]=0
    条件不成立
最大得票数を持つ政党: B党 (得票数=660)
B党の議席が増加。再計算後のHikaku[1] = 330.0
現在のTosen = [1, 1, 2, 0]
----------------------------------------
議席確定数: 4/6
現在のHikaku = [600.0, 330.0, 480.0, 180]
現在のTosen = [1, 1, 2, 0]
現在のKoho  = [5, 4, 2, 3]
ループ開始。最大得票数を探します。
  政党: A党, 現在の最大値: 0, Hikaku[0]=600.0, Koho[0]=5, Tosen[0]=1
    条件成立: max < Hikaku[0] かつ Koho[0] >= Tosen[0] + 1
  政党: B党, 現在の最大値: 600.0, Hikaku[1]=330.0, Koho[1]=4, Tosen[1]=1
    条件不成立
  政党: C党, 現在の最大値: 600.0, Hikaku[2]=480.0, Koho[2]=2, Tosen[2]=2
    条件不成立
  政党: D党, 現在の最大値: 600.0, Hikaku[3]=180, Koho[3]=3, Tosen[3]=0
    条件不成立
最大得票数を持つ政党: A党 (得票数=600.0)
A党の議席が増加。再計算後のHikaku[0] = 400.0
現在のTosen = [2, 1, 2, 0]
----------------------------------------
議席確定数: 5/6
現在のHikaku = [400.0, 330.0, 480.0, 180]
現在のTosen = [2, 1, 2, 0]
現在のKoho  = [5, 4, 2, 3]
ループ開始。最大得票数を探します。
  政党: A党, 現在の最大値: 0, Hikaku[0]=400.0, Koho[0]=5, Tosen[0]=2
    条件成立: max < Hikaku[0] かつ Koho[0] >= Tosen[0] + 1
  政党: B党, 現在の最大値: 400.0, Hikaku[1]=330.0, Koho[1]=4, Tosen[1]=1
    条件不成立
  政党: C党, 現在の最大値: 400.0, Hikaku[2]=480.0, Koho[2]=2, Tosen[2]=2
    条件不成立
  政党: D党, 現在の最大値: 400.0, Hikaku[3]=180, Koho[3]=3, Tosen[3]=0
    条件不成立
最大得票数を持つ政党: A党 (得票数=400.0)
A党の議席が増加。再計算後のHikaku[0] = 300.0
現在のTosen = [3, 1, 2, 0]
----------------------------------------
最終結果:
A党: 3名
B党: 1名
C党: 2名
D党: 0名

おお、すべての議席が決まるまでの処理が表示された。選挙のように結果が大きく影響するものでは、正確な処理が求められるから、ログを使ってバグが入らないようにする必要がありますね！

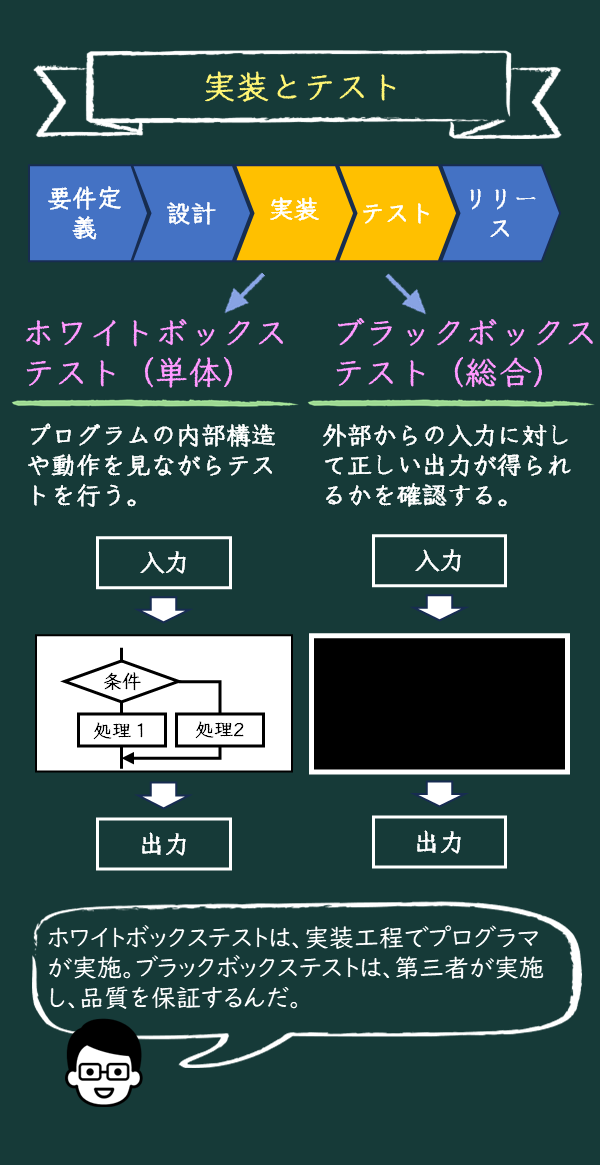
ホワイトボックステストとブラックボックステスト

そうだね。プログラムの内部構造やコードの流れを検証するためにもログは使われるよ。こうしたテストをホワイトボックステストって呼ぶんだよ。

ホワイトボックス？どういう意味ですか。

ホワイトボックスという名前は、プログラムの内部が透明な箱（ホワイトボックス）のように見えることからきているんだ。つまり、中身がすべて見えている状態でテストするってことだよ

なるほど！このテストは、前回の授業で説明してもらった「ウォーターフォール開発」の中の、どの工程で実施するんですか

ここまでは「実装（プログラミング）」工程で実施するんだ。プログラム単体で実施することから「単体テスト」と呼ぶよ。

なるほど！じゃあ「ウォーターフォール開発」の「テスト」工程ではどんなテストを行うんですか

「テスト」工程では、複数のモジュールやプログラム全体が連携して正しく動作するかを確認するよ。これを「総合テスト」と呼ぶよ。

もしかして、総合テストは「ブラックボックステスト」ですか？

鋭いね。総合テストは 内部構造は考慮せず、外部の仕様に限定したテストなので、「ブラックボックステスト」とも呼ばれる。プログラミングをした人とは別の第三者が実施することが望ましいんだ。

「単体テスト」は中身を見て「ホワイトボックス」で、「総合テスト」は中身を隠して「ブラックボックス」で実施するんですね。違いがよくわかりました！

その通り！開発の品質を守るために、こうした段階的なテストが欠かせないんだ。

まとめ

問題

「クイズをスタート」のボタンをクリックすると、５問出題します。さあチャレンジ！

編集者ひとこと

サンプル問題第２問を３回に分けて解説しましたが、解きごたえありましたね。
これからの大学生は、これくらいのプログラミングができるようになっているとすると、将来の日本は明るい！。もちろん、それを迎える社会のほうもレベルを上げていかないければいけません。頑張りましょう！