問題
問題文
| 出典:独立行政法人大学入試センター 公開問題「平成30 年告示高等学校学習指導要領に対応した令和7年度大学入学共通テストからの出題教科・科目 情報サンプル問題」 https://www.mext.go.jp/content/20211014-mxt_daigakuc02-000018441_9.pdf |
問2 次の文章を読み,空欄 (オカ) ~ (クケ) に当てははまる数字をマークせよ。
鈴木さんは,図1 から,1試合当たりの得点とショートパス本数の関係に着目し,さらに詳しく調べるために,1試合当たりの得点をショートパス本数で予測する回帰直線を,決勝進出チームと予選敗退チームとに分けて図2のように作成した。

鈴木さんは,この結果からショートパス100 本につき,1試合当たりの得点増加数を決勝進出チームと予選敗退チームで比べた場合,0. (オカ) 点の差があり,ショートパスの数に対する得点の増加量は決勝進出チームの方が大きいと考えた。
また,1試合当たりのショートパスが320 本のとき,回帰直線から予測できる得点の差は,決勝進出チームと予選敗退チームで,小数第3位を四捨五入して計算すると,0.0 (キ) 点の差があることが分かった。鈴木さんは,グラフからは傾きに大きな差が見られないこの二つの回帰直線について,実際に計算してみると差を見つけられることが実感できた。
さらに,ある決勝進出チームは,1試合当たりのショートパス本数が384.2 本で,1試合当たりの得点が2.20 点であったが,実際の1試合当たりの得点と回帰直線による予測値との差は,小数第3位を四捨五入した値で0. (クケ) 点であった。
解答
- (オカ)の解答 16
- (キ)の解答 4
- (クケ)の解答 56
解説
今回の授業は回帰分析を学びます。回帰分析とは、調べたいデータの項目間の関係性を回帰直線という数式にして、現状の傾向の把握や予測を行う分析手法です。
回帰直線の変数を入れてみて、結果を確認することで、データ分析の重要性を理解していきましょう。
黒板
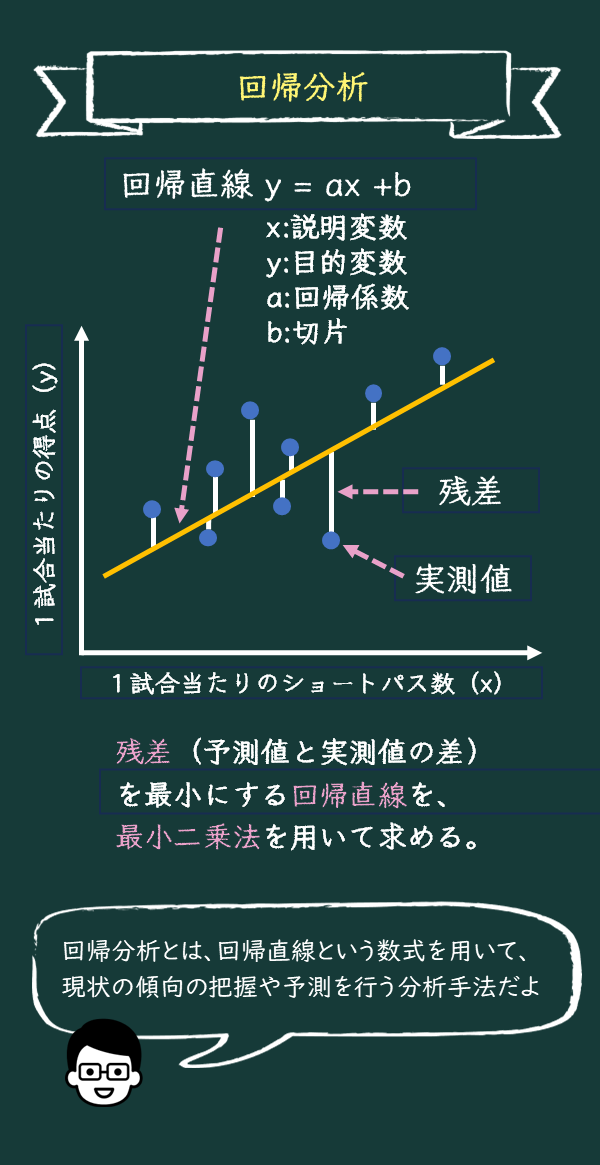
回帰直線とは何か

回帰分析って聞いたことあるかな?

回帰分析?初めて聞きました。

回帰分析は、調べたいデータの項目間の関係性を回帰直線という数式にして、現状の傾向の把握や予測を行う分析手法だよ。

回帰直線?一体どんな数式ですか?

回帰直線は「y=ax+b」で表される一次関数だよ。「a」は回帰係数、「b」が切片だよ。この回帰係数がxとyの関係を表しているんだ。

なるほど。一次関数なら中学で勉強しました。「x」とか「y」は変数ですよね。これは呼び方はあるんですか?

いい質問だね。回帰直線における「x」は説明変数、「y」を目的変数と呼ぶよ。

説明変数、目的変数?

まず、説明変数「x」は、「y」の動きに「影響を与える側の変数」だから、「説明する変数」として説明変数と呼ばれているんだ。

なるほど、yの変化を説明するための変数ということですね。

次に、目的変数「y」は、「最終的に知りたい値」や「予測したい値」だから、「目的」という名前がついているんだ。つまり、目的変数は説明変数に影響されて変わる変数で、回帰分析ではその目的変数を予測することが目的なんだよ。

なるほどね。回帰直線が「y=ax+b」で表せるから、回帰係数「a」の値が大きいと、説明変数が、目的変数に強く影響することになるんですね?

その通り。よく理解しているね。回帰直線を使うと、まだ見てないデータの予測もできるんだ。

未来を予測をできるなんてすごい!回帰直線を使わないわけにいきませんね
回帰直線からAIへ

そうだね。でも、回帰直線が万能というわけじゃないんだ。すべてのデータがきれいに回帰直線に当てはまるわけではなく、実際にはより複雑な要因が絡み合っていることも多いんだよ。,

え、もっとややこしい曲線ということですか?

そうだね。説明変数が1つの回帰分析を単回帰分析、複数ある場合は重回帰分析と呼ぶんだ。重回帰分析はAIにも使われているよ。

最新のChat GPTは兆を超えるパラメーター数を持つというよう話を聞いたことがありますが、これと関係ありますか?

うん、関係があるよ。回帰直線では、1つの説明変数 x に対して1つの回帰係数があるけど、AIのモデルはもっと大量のデータを扱えるように、たくさんの説明変数や回帰係数を持っているんだ。

つまり、AIのパラメーターっていうのは、回帰直線の係数「a」 がたくさんあるようなイメージなんですね!

その通り!でも、どんなにたくさんのパラメーターがあっても、基本は回帰直線と同じで「データからパターンを学習して、未来や未知のデータを予測する」という考え方が土台なんだ。

そう考えると、今回の授業で学んだことが、すごく深いところまでつながっているんですね!
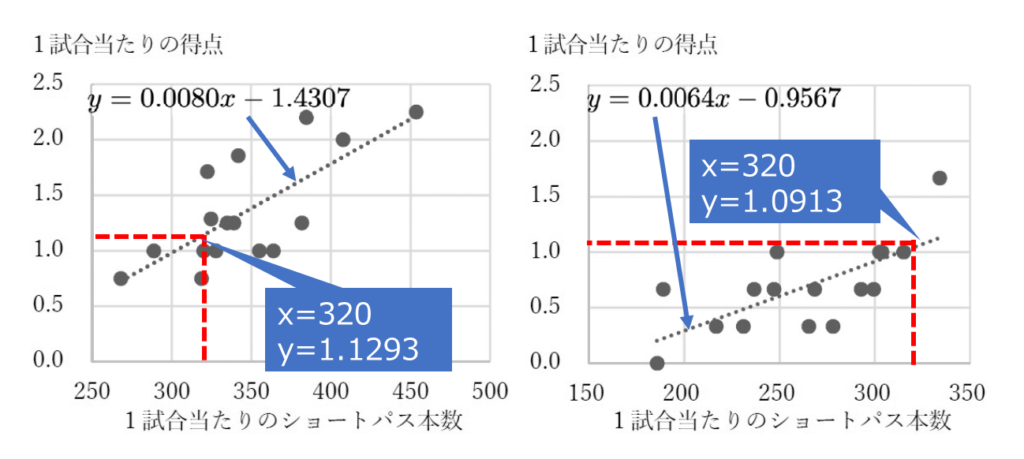
1 試合当たりの得点とショートパス本数の回帰直線
| 決勝進出チームの回帰直線 y=0.0080x-1.4307 予選敗退チームの回帰直線 y=0.0064x-0.9567 |

「1試合当たりの得点をショートパス本数で予測する回帰直線を、決勝進出チームと予選敗退
チームとに分けて作成した」と書いてありますね。この式を見て、何が分かるんですか?

回帰直線は「y = ax + b」で表されるといったよね。ここで、「y」、「x」はなんの変数かな?

「y」は、1試合当たりの得点、「x」は一試合当たりのショートパスの本数じゃないですか?

いいね。では「a」の回帰係数に該当する値は何かな?

決勝進出の回帰係数aは「0.0080」ですね。

ここで「x」のショーパスが1本増えると、「y」の得点はどれだけ増えるということを意味するかな?

決勝進出チームでは、「0.0080」ですね。そうか!決勝進出チームだとショートパス1本増えると「0.0080点」得点が増えるってことですね。

その通り!一方、予選敗退チームだと「0.0064点」しか増えない。つまり、ショートパスが増えたときの得点への影響は、決勝進出チームの方が大きいんだよ。

なるほど!ショートパスの数が多いほど決勝進出チームの方が有利になるってことですね。じゃあ、「b」の切片つまり、「-1.4307」とか「-0.9567」は何を意味していますか?

ショートパスがゼロのときの得点を示しているんだ。実際の試合ではショートパス以外の要素もたくさん影響するから、今回の結果ではマイナスになっているんだ。

回帰直線を使うと、ショートパスの本数から得点を予測できるんですね。これで、どれくらいショートパスを増やせば得点も増えるか、戦略が立てやすくなりそうですね!

その通り!データに基づいて未来の結果を予測できるのが、回帰直線の大きな価値なんだよ。
ショートパス100本ごとの得点増加量
| 鈴木さんは、この結果からショートパス100本につき、1試合当たりの得点増加数を決勝進出チームと予選敗退チームで比べた場合、0. (オカ)点の差があり、ショートパスの数に対する得点の増加量は決勝進出チームの方が大きいと考えた。 |

じゃあ、ショートパス100本ごとにどれくらい得点が増えるかを計算してみよう。

回帰係数は、「ショートパス1 本につき、1試合当たりの得点増加数」だったから、これに100をかければよさそうですね。

いいね。早速計算してみよう。

決勝進出チームの回帰係数が0.0080だから「0.0080 × 100 = 0.8」、予選敗退チームの回帰係数は0.0064だから「0.0064 × 100 = 0.64」ですね。

では両者の増加量の差はどうなる?

「0.8 – 0.64 = 0.16」。(オカ)の答えは16ですね。

正解!正の値になっているので、鈴木さんの「ショートパスの数に対する得点の増加量は決勝進出チームの方が大きいと考えた」という考えと一致しているね。
ショートパス320本の時の得点差
| 1試合当たりのショートパスが320本のとき、回帰直線から予測できる得点の差は、決勝進出チームと予選敗退チームで、小数第3 位を四捨五入して計算すると、0.0(キ)点の差があることが分かった。 |

ショートパスが320本だったとき、決勝進出チームと予選敗退チームで得点にどれくらいの差が出るかを計算してみようか。

まず決勝進出チームの回帰式にX=30を代入すればよいですね。y = 0.0080 × 320 – 1.4307= 1.1293点ですね。

良いね。じゃあ、次に予選敗退チームの予測得点を計算してみて。

予選敗退チームは、y = 0.0064 × 320 – 0.9567= 1.0913点です。

うん、その差を小数第3 位を四捨五入して計算してみよう。

差は「1.1293 – 1.0913 = 0.038」点。少数第3位を四捨五入して「0.04点」。(キ)の答えは「4」です。

完璧!
実際の得点と予測得点の差
| ある決勝進出チームは、1試合当たりのショートパス本数が384.2本で、1試合当たりの得点が2.20点であったが、実際の1試合当たりの得点と回帰直線による予測値との差は、小数第3位を四捨五入した値で0.(クケ)点であった。 |

決勝進出チームだから、「y=0.0080x-1.4307」の式に、x=384.2を代入すればいいんだね。

いいね。yの値はどうなるかな?

y = 0.0080 × 384.2 – 1.4307= 1.6429点ですね。あれ、問題では「1試合当たりの得点が2.20点」とあるけれど、なんで一致しないの?

よく気づいたね。実際の得点と予測値が一致しないのは、回帰直線がデータの傾向を表しているだけで、すべてのデータ点が完全にその直線上に乗るわけではないからなんだ。

なるほど、だからズレが出るんですね。でも、このズレってどうして起きるんですか?

いい質問だね。このズレは「残差」と言って、回帰直線が表すのはあくまで全体の傾向なんだ。だから、ある試合では予測より得点が高くなることもあれば、低くなることもある。この残差が小さいほど、予測が実際に近いと言えるんだよ。

じゃあ、今回の場合の残差って、「2.20点 – 1.6429点 = 0.5571点」ってことですね。

その通り!、これを小数第3位を四捨五入した値するとどうなるかな?

「0.56点」ですね。「クケ」の答えは「56」になりますね。

相関係数と回帰直線の関係

ところで先生、前回習った相関係数と、今回習った回帰係数はどういう関係があるんですか?どちらも2つの項目の関係を数値で示すものですよね?

いい質問だね!確かにどちらも2つの項目の関係を表す数値だけど、役割が少し違うんだよ。相関係数は、2つの変数がどれだけ「強く」関係しているか、つまり一緒に変化する傾向がどのくらいあるかを示しているんだ。

そうでしたよね。回帰係数も同じような気もしますが・・。

回帰係数は、相関関係を使って「予測」をするためのものなんだ。相関係数が高い場合、データの点が回帰直線に近い位置に集まることが多いということなんだ。つまり全体的に残差が少ないということだよ。

なるほど!相関係数が高いと、データが回帰直線に近くなるから残差が小さいんですね。でもどうやって、全体的に残差を小さくするんですか?

いい質問だね。実は、回帰直線を引くときに使う「最小二乗法」っていう方法が、残差をできるだけ小さくするために使われるんだよ。

最小二乗法?

最小二乗法は、回帰直線をデータに最も近づけるために、残差を小さくするように計算するんだ。残差はプラスもマイナスもあるから、二乗して全部足し合わせ、この値が一番小さくなるように直線の傾きと切片を決めるんだよ。

残差を二乗することで、すべてのズレをプラスにして合計し、全体として最もズレが少ない直線を見つけられるんですね。

その通り!データの点がたくさんあっても、最小二乗法を使えば、データ全体の傾向に最もよく当てはまる回帰直線が引けるんだよ。これがデータの予測や分析に役立つわけだね。

なるほど、回帰直線ってデータの平均的な傾向を表していて、それを使って未来の値を予測できるんですね!

そうだね。相関係数が高いほど、データのばらつきが少ないから、回帰直線の予測もより信頼性が高くなるんだよ。
プログラミング

今回もGoogle Colaboratoryを使ってグラフを作ってみよう。Google Colaboratoryについては、以前(45.データの整形と修正)詳しく解説しているので、はじめてのまずそちらから見てね。

はい、今回は何のデータを使って分析するんですか?

前回と同様に、2023年のJリーグのデータを使ってみよう。入手元などは前回の授業を見てください。

このデータから、1試合平均得点数と、1試合平均パス数の回帰直線を描くんですね。

その通り。回帰直線以外の他に、相関係数も求めるよ。

面白そう!
回帰直線の表示
# 必要なライブラリをインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# データをファイルパスから直接読み込む
file_path = 'J1league_all_2023_ENG.csv' # ここにファイルパスを指定してください
data = pd.read_csv(file_path)
# 列名を英語にリネーム
data = data.rename(columns={
'チーム名': 'Team Name',
'1試合平均得点数': 'Average Goals per Game',
'1試合平均パス数': 'Average Passes per Game',
'トップ9': 'Top 9'
})
# 必要なカラムのみフィルタリング
data_filtered = data[['Team Name', 'Average Goals per Game', 'Average Passes per Game', 'Top 9']]
# トップ9チームとその他のチームのデータを分ける
top_9_teams = data_filtered[data_filtered["Top 9"] == 1]
other_teams = data_filtered[data_filtered["Top 9"] == 0]
# 回帰直線を計算する関数
def calculate_regression(X, y):
X_reshaped = X.values.reshape(-1, 1) # Xを2次元配列に変換
model = LinearRegression().fit(X_reshaped, y) # 回帰モデルをフィッティング
regression_line = model.predict(np.linspace(X.min(), X.max(), 100).reshape(-1, 1)) # 回帰直線を計算
return model, regression_line
# トップ9チームの回帰直線と相関係数を計算
model_top9, line_top9 = calculate_regression(top_9_teams["Average Passes per Game"], top_9_teams["Average Goals per Game"])
correlation_top9 = np.corrcoef(top_9_teams["Average Passes per Game"], top_9_teams["Average Goals per Game"])[0, 1]
# その他のチームの回帰直線と相関係数を計算
model_other, line_other = calculate_regression(other_teams["Average Passes per Game"], other_teams["Average Goals per Game"])
correlation_other = np.corrcoef(other_teams["Average Passes per Game"], other_teams["Average Goals per Game"])[0, 1]
# トップ9チーム用のグラフを描画
plt.figure(figsize=(10, 6))
plt.scatter(top_9_teams["Average Passes per Game"], top_9_teams["Average Goals per Game"], color='blue', label='Top 9 Teams')
# 回帰直線を描画
plt.plot(np.linspace(top_9_teams["Average Passes per Game"].min(), top_9_teams["Average Passes per Game"].max(), 100), line_top9, color='blue',
label=f'Regression: y = {model_top9.coef_[0]:.4f}x + {model_top9.intercept_:.2f}, Corr = {correlation_top9:.4f}')
# チーム名をマーカーの上部に表示
for i, team in enumerate(top_9_teams['Team Name']):
plt.text(top_9_teams["Average Passes per Game"].values[i],
top_9_teams["Average Goals per Game"].values[i] + 0.02, # 少し上に配置するために +0.02 を追加
team, fontsize=9, color='blue')
# グラフの設定
plt.title('Average Goals per Game vs Average Passes per Game (Top 9 Teams)')
plt.xlabel('Average Passes per Game')
plt.ylabel('Average Goals per Game')
plt.legend()
plt.grid(True)
plt.show()
# その他のチーム用のグラフを描画
plt.figure(figsize=(10, 6))
plt.scatter(other_teams["Average Passes per Game"], other_teams["Average Goals per Game"], color='red', label='Other Teams')
# 回帰直線を描画
plt.plot(np.linspace(other_teams["Average Passes per Game"].min(), other_teams["Average Passes per Game"].max(), 100), line_other, color='red',
label=f'Regression: y = {model_other.coef_[0]:.4f}x + {model_other.intercept_:.2f}, Corr = {correlation_other:.4f}')
# チーム名をマーカーの上部に表示
for i, team in enumerate(other_teams['Team Name']):
plt.text(other_teams["Average Passes per Game"].values[i],
other_teams["Average Goals per Game"].values[i] + 0.02, # 少し上に配置するために +0.02 を追加
team, fontsize=9, color='red')
# グラフの設定
plt.title('Average Goals per Game vs Average Passes per Game (Other Teams)')
plt.xlabel('Average Passes per Game')
plt.ylabel('Average Goals per Game')
plt.legend()
plt.grid(True)
plt.show()



じゃあ、Google Colaboratoryを使ってグラフを作ってみよう。

Google Colaboratoryにデータを読みこんで、Pythonのプログラムコードを実行してみます。おっ!出てきました。

上位9チームが上のグラフ(青)、下位9チームが下のグラフ(赤)だよ。ここからリンクしているから見てね。

上位9チームの、回帰直線の式は y=0.0021x + 0.42ですね。この後に書かれているCorr=0.4834というのは何ですか?

これは相関係数だね。相関係数は -1 から 1 までの値を取るんだけど、0.4834 は中程度の相関を示しているんだ。

たしかに、回帰直線から外れている点がいくつかありますね。優勝したヴィッセル神戸は、パスが少ないけれども得点は多い。2位の横浜F・マリノスはパスが多くて得点も多い。

下位9チームはどうだろう

下位9チームの、回帰直線の式は y=0.0007x + 0.88ですね。こちらの相関係数は 0.2780だから、あまり相関がなさそうですね。
回帰直線の信頼性

相関係数は、回帰直線がどれだけデータに合っているかを判断するために重要な指標であることが分かったかな?

はい。相関係数を確認することで、回帰直線がどれくらい信頼できるのかを判断したほうがよいんですね。

その通り。例えば、0.2780 のように低い相関係数だと、回帰直線がデータの傾向をあまりよく表していないことを示しているんだ。

なるほど。じゃあ、下位9チームの相関係数が低いということは、パス数と得点の関係があまり強くなく、他の要因が影響している可能性があるってことですね。

そうだね!サッカーのパフォーマンスは、パスや得点だけでなく、他にも多くの要因が関わってくる。相関係数を使うことで、どの要因が強く影響しているのかを見極める手がかりになるんだよ。

次は他のデータでも相関を調べてみたいです!パス数や得点以外にも何か関係があるかもしれませんね。

いいね!データ分析は、必ずしも期待する結果が得られないこともあるから、その時はその理由もしっかり考察してみることが大切だよ。
まとめ
- 回帰直線
回帰直線とは、2つの変数の関係を表す線で、過去のデータから未来の結果を予測するために使われる。 - 回帰直線の式
回帰直線の式は「y = ax + b」で表される。この式で、aは回帰係数、bは切片を指す。 - 回帰係数
xが1増えたときにyがどれだけ増えるかを示す数値である。 - 残差
回帰直線で予測された値と実際のデータとのズレである。残差が小さいほど予測が正確である。 - 最小二乗法
データと回帰直線のズレを二乗してその合計を最小にすることで、回帰直線を求める方法である。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジF!
編集者ひとこと
AI研究の第一人者である東京大学の松尾先生は、「深層学習とは、最小二乗法の巨大なお化けのようなものだ」と紹介しています。深層学習とは今の生成系AIでも使われている技術です。
回帰直線であれば、説明変数xと目的変数yの関係が見てわかるけれど、今の生成系AIのように知識を持っているような予測ができるというのは、信じられないですよね。興味がある人は、AIの専門書を読んでみてくださいね。
<RANKING>![]()
高校教育ランキング



