問題
問題文
| 出典：独立行政法人大学入試センター 公開問題「平成30 年告示高等学校学習指導要領に対応した令和7年度大学入学共通テストからの出題教科・科目 情報サンプル問題」 https://www.mext.go.jp/content/20211014-mxt_daigakuc02-000018441_9.pdf |
第3問 次の文章を読み，後の問い( 問１～４)に答えよ。
S高等学校のサッカー部のマネージャーをしている鈴木さんは、「強いサッカーチームと弱いサッカーチームの違いはどこにあるのか」というテーマについて研究している。鈴木さんは、ある年のサッカーのワールドカップにおいて、予選で敗退したチーム（予選敗退チーム）と、予選を通過し、決勝トーナメントに進出したチーム（決勝進出チーム）との違いを、データに基づいて分析することにした。このデータで各国の代表の32チームの中で、決勝進出チームは16チーム、予選敗退チームは16チームで
あった。
分析対象となるデータは、各チームについて、以下のとおりである。
●試合数… 大会期間中に行った試合数
●総得点… 大会で行った試合すべてで獲得した得点の合計
●ショートパス本数… 全試合で行った短い距離のパスのうち成功した本数の合計
●ロングパス本数… 全試合で行った長い距離のパスのうち成功した本数の合計
●反則回数… 全試合において審判から取られた反則回数の合計
鈴木さんは、決勝進出チームと予選敗退チームの違いについて、このデータを基に、各項目間の関係を調べることにした。データの加工には、表計算ソフトウェアを活用し、表1のデータシートを作成した。
決勝進出チームと予選敗退チームの違いを調べるために、決勝進出の有無は、決勝進出であれば1、予選敗退であれば0とした。また、チームごとに試合数が異なるので、各項目を1試合当たりの数値に変換した。
また，データシートを基に，統計処理ソフトウェアを用いて，図１を作成した。
図１のⅠ～Ⅳは，それぞれの項目の全参加チームのヒストグラムを決勝進出チームと予選敗退チームとで色分けしたものであり，(1)～(4)は決勝進出チームと予選敗退チームに分けて作成したヒストグラムである。あ～かは，それぞれの二つの項目の全参加チームと決勝進出チーム，予選敗退チームのそれぞれに限定した相関係数である。またA～F は，それぞれの二つの項目の散布図を決勝進出チームと予選敗退チームをマークで区別して描いている。例えば，図１のA は縦軸を「１試合当たりの得点」，横軸を「１試合当たりのショートパス本数」とした散布図であり，それに対応した相関係数はあで表されている。
問１ 次の問い（ａ・ｂ）に答えよ。
ａ. 次の文章を読み，空欄 ア ～ ウ に入れる最も適当なものをそれぞれの解答群のうちから一つずつ選べ。ただし，空欄 ア ・ イ の順序は問わない。
図１を見ると，予選敗退チームにおいてはほとんど相関がないが，決勝進出チームについて負の相関がある項目の組合せは，１試合当たりの （ア ）と（イ） である。また，決勝進出チームと予選敗退チームとで，相関係数の符号が逆符号であり，その差が最も大きくなっている関係を表している散布図は （ウ） である。したがって，散布図の二つの記号のどちらが決勝進出チームを表しているかが分かった。
ｂ.図１から読み取れることとして誤っているものを解答群から一つ選べ。 エ
解答群
解答
- （ア）、（イ）の解答 (0) 得点、 (3)反則回数 （順不同）
- （ウ）の解答 (3) D
- （エ）の解答 (2) 全参加チームについて正の相関がある項目の組合せの中には，決勝進出チーム，予選敗退チームのいずれも負の相関となっているものがある。
解説
今日は「散布図」と「相関係数」の基礎を学び、実際に分析を行います。生徒はパス数やファウル数のデータからチームの戦略を考察し、相関関係と因果関係の違いについても理解を深めます。
黒板
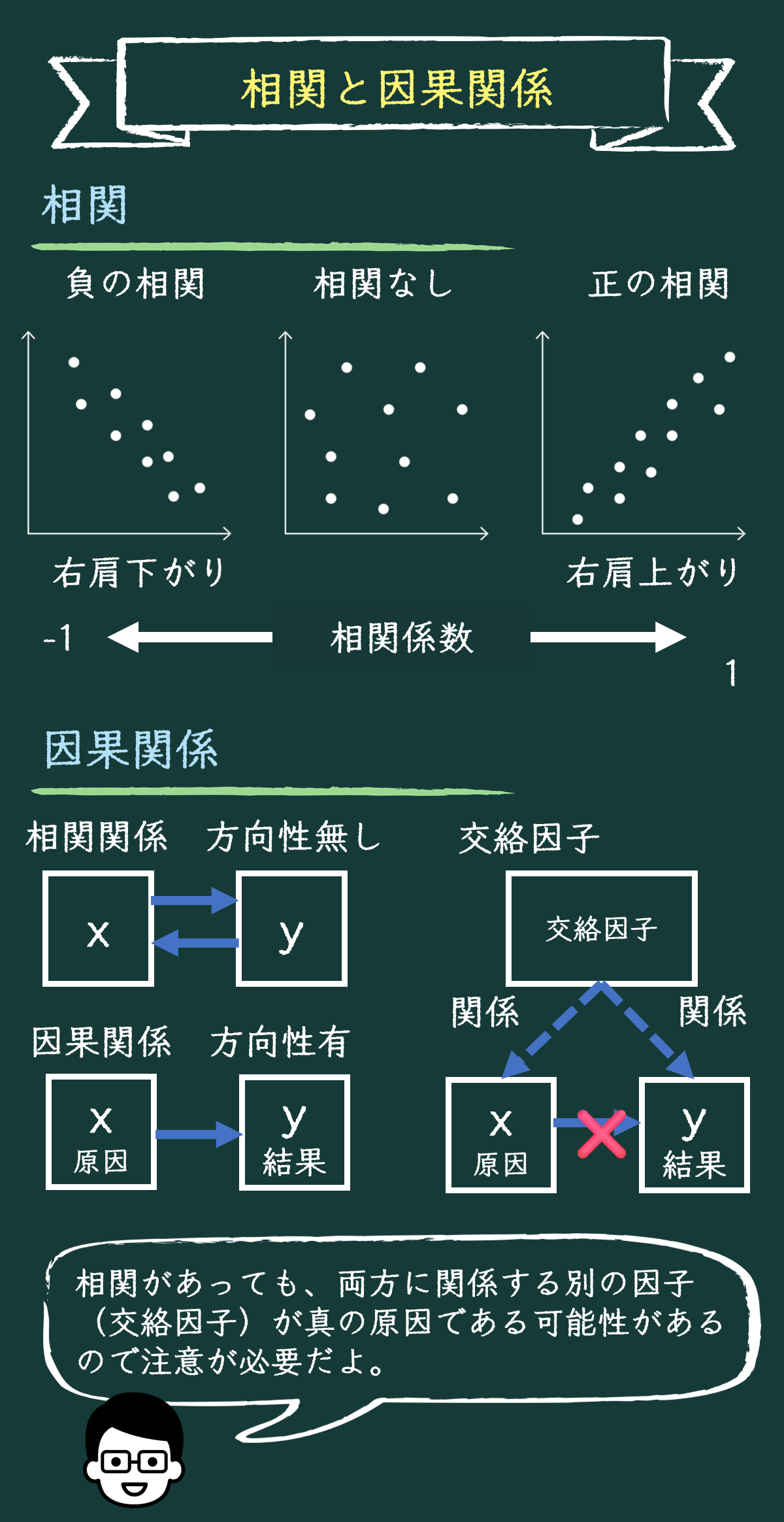
散布図と相関係数の基礎
今回の問題では「散布図」と「相関係数」についてしっかり理解することがポイントだよ。
散布図って、ただ点がいっぱい並んでるように見えるんですけど、それで何が分かるんですか？
散布図では、点のばらつき具合から2つの項目の間に関係があるかどうかを見ていくんだ。
関係？なんの関係ですか？
相関図で点が右上がりになっていれば「正の相関」があるといい、相関係数がプラスになるんだ。
相関係数？
相関係数は、2つのデータの間にどれくらい強い関係があるかを数値で表すものなんだ。
２つの項目の関係を数字で表せるんですか？
そうなんだ。たとえば、1に近ければ近いほど「この2つのデータは一緒に増えたり減ったりしている」っていう強い関係があることになるんだよ。
なるほど！もしかして、「負の相関」というものもあるんですか？
いいところに気づいたね！「負の相関」というのは、2つのデータが逆の動きをするときに使うんだ。つまり、片方が増えるともう片方が減る、という関係だよ。相関係数は-1に近いほど、この負の相関が強いということになるんだ。
なるほど、じゃあ、相関係数が0に近い場合はどうなりますか？
相関係数が0に近いと、2つのデータの間にはほとんど関係がない、ということを表しているんだ。グラフで見ると、点がバラバラに散らばっていて、特に右上がりや右下がりのパターンが見られない場合だね。
点がバラバラなら、相関はないってことなんですね。少しずつ分かってきました！
問1-a 散布図と相関係数を読む
| 決勝進出チームについて負の相関がある項目の組合せは、1試合当たりの（ア）と（イ）である。 |
「決勝進出チームについて負の相関がある項目の組み合わせは」を聞いていますね。どうやって見分ければいいんですか？
良い質問だね。まず、負の相関があるというのは、どういうことだったか覚えているかな？
相関係数は-1に近いほど負の相関があるんでしたよね。でも、図１のどこを見れば、相関係数がわかるんですか？この図の見かたがさっぱりわかりません。
図1の散布図では、縦軸と横軸にそれぞれ項目が割り当てられていて、その組み合わせで2つの項目の関係を表しているんだ。
なるほど。例えば、「あ」は「一試合当たりの得点」と「1試合当たりのショートパス本数」の間の相関を表しているということですね。
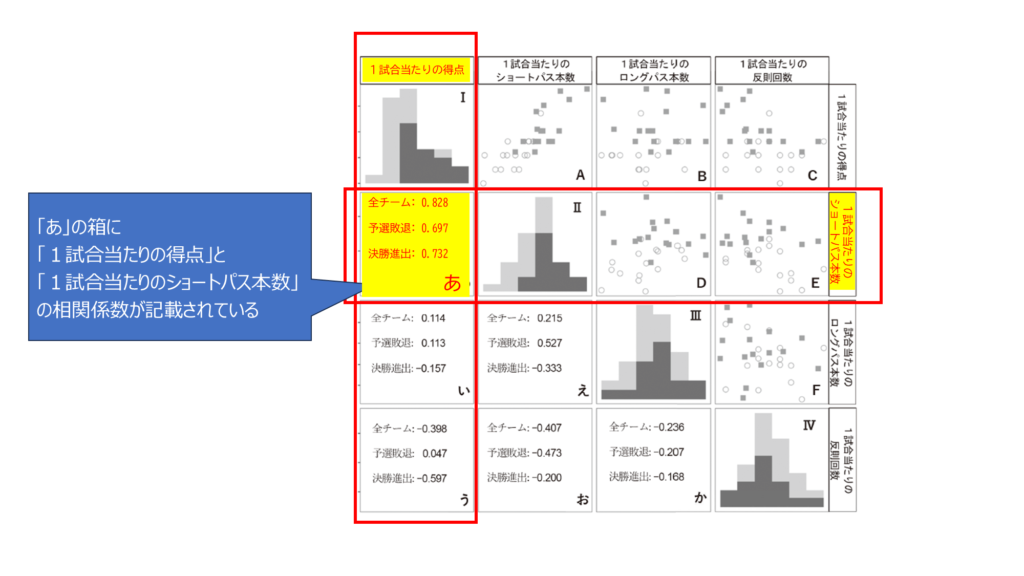
その通り！じゃあ、「あ」～「か」の中で、「決勝進出」の値が、マイナス１に近いものはどれかな？
「う」の-0.597ですね。これは、えーと「1試合当たりの得点」と「1試合当たりの反則回数」の相関ですね。
その通り！負の値をとる組み合わせは他にもあるけれど、ほかの値は０に近いので強い負の相関がある」とは言い切れない値だね。
なるほど。でも得点が多ければ多いほど、反則は少ないというというのは、なんか逆な気がする。反則が少なければ、得点が多いというのならわかるけど。
相関関係と因果関係の違い
いいところに気づいたね。ここで大事なのが、「相関」と「因果」の違いなんだ。
「相関」と「因果」？
相関というのは、2つの項目の間に何らかの関係があることを示しているだけで、一方が他方を直接引き起こしているとは限らないんだよ。
ん？？
「反則が少ないから得点が多い」かもしれないし、逆に「得点が多いと反則を受けにくい」かもしれないし、実は他の要因が絡んでいるかもしれないんだ。相関があると、あくまで「2つが一緒に動いている」ということがわかるだけなんだよ。
なるほど、だから「負の相関」があっても、それが原因と結果を意味するわけじゃないんですね！
そうだね。だからデータ分析では、相関を見つけることは大事だけど、次に「なぜその相関があるのか」をしっかり考える必要があるんだよ。
なるほど！データって奥が深いですね。
| また、決勝進出チームと予選敗退チームとで、相関係数の符号が逆符号であり、その差が最も大きくなっている関係を表している散布図は（ウ）である |
相関係数の見方が分かったから、よくデータを見れば答えられるはずだよ。
えっ。相関係数が逆符号のものは、「い」の「0.113、?0.157」、「う」の「0.047、? 0.597」、「え」の「0.527、?0.333」の3つですね
いいね。じゃあ、その差が最も大きいものは？
それぞれの差を計算すればよいのですね。「い」は0.27、「う」は0.644、「え」は0.86だから、一番大きいのは「え」ですね。
相関係数を用いた仮設立案
いいね。では「え」の箱に書かれている相関関係から何が言えるか考えてみよう。
予選敗退しているチームは、「ロングパス本数」と「ショートパス本数」に正の相関が強い。一方で決勝進出しているチームは負の相関があるということですね。
よく観察してるね。ここからのどんな分析ができるかな？
予選敗退チームはロングパスとショートパスを一緒に多用している。つまり「無秩序に攻撃している可能性」のかもしれませんね。
おお！
決勝進出チームは、状況によってショートパスを多用するか、あるいはロングパスで一気に展開するかを的確に判断しているんでしょうね。
専門家みたいだね。今のところこの分析は、仮説だけれども、それを実践で検証して成果が出るかどうか試してみたくなるよね。
そうですね。監督にとってはこういったデータは貴重ですね。
散布図の見方
さて、先ほどの問1-a（ウ）の解答はどうなるかな？
さっき回答した通り、「え」です。あれ、解答群に「え」がないですよ？誤記ですかね？
問題をよく見て。「その差が最も大きくなっている関係を表している散布図は？」と聞いているよね
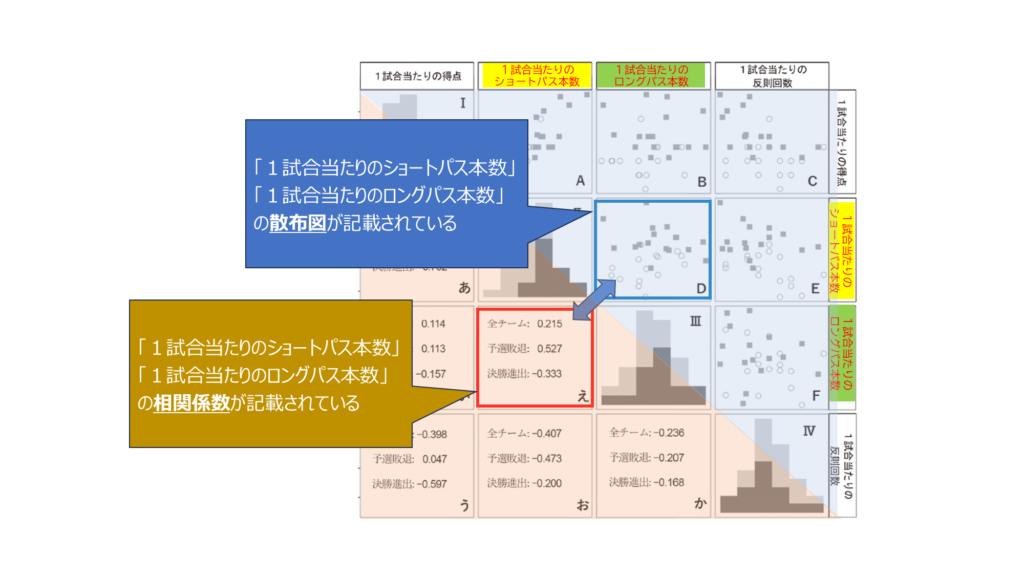
ああ、やられた。（え）は相関係数でしたね。でも、「え」に該当する、散布図はどれを見ればよいんだろう？
このグラフの左上から右下に線を引いて、ちょうど対角線上にあるグラフが、該当の散布図だよ。
ということは「D」ということかな？どうしてそうなるの？
「D」の横軸と縦軸は何の項目が書いてあるかな？
横軸が「1試合当たりのロングパス本数」、縦軸が「1試合当たりのショートパス本数」ですよね。
じゃあ「え」の相関関係は何を示していたっけ？
横軸が「1試合当たりのショートパス本数」、縦軸が「1試合当たりのロングパス本数」ですよね。あれ、縦横が反対になっているだけだ。
そうだね。2つの項目の関係を見ているのだから、縦軸と横軸は逆でも同じ意味ということなんだ。だからこの散布図は対角線から上半分を散布図、下半分を相関図にしているんだ。
そうやってみるんですね。
問題文にも「例えば、図1のAは縦軸を「1試合当たりの得点」、横軸を「1試合当たりのショートパス本数」とした散布図であり、それに対応した相関係数はあで表されている」。と書いてあるよね。
説明されて、問題文に書かれたこの説明が理解できました。
問1-b – 正誤問題の解説
次は問1-bだね。この問題では、図1から読み取れる情報の中で誤っているものを選ぶ問題だ。選択肢を一つずつ確認していこうか。
| （０）「決勝進出チームは黒い四角形（■）、予選敗退チームは白い円（○）」で表されている |
普通は、グラフの「凡例」として■や〇の意味があるはずですよね。これは記載ミスじゃないですか？
ははは、そういいたくなるのはわかるけれど。書いていなくても、データから読み取れるよ。ヒントは「a」の問題文にあるよ
「したがって、散布図の二つの記号のどちらが決勝進出チームを表しているかが分かった」というところですか？分かったことことになっているみたいですけれど、私にはさっぱりわかりません。
Dをよく見てみて。〇はどういう相関があるかな？
うーん、なんとなく右上がりにも見えます。つまり「正の相関」があるみたいです。
では「う」の相関関係で、「正の相関」があったのは、「予選敗退」チーム、「決勝進出」チームのどちらかな？
「予選敗退」チームですね。じゃあ「〇」は予選敗退チームということですね。「? それぞれの散布図の中で、決勝進出チームは黒い四角形（■）、予選敗退チームは白い円（〇）で表されている。」は、正しいということですね。
相関関係の読み取り
| （１）全参加チームを対象としてみたとき、最も強い相関がある項目の組合せは1試合あたりの得点 と1 試合あたりのショートパス本数である。 |
その通り！次は(1)だね。早速グラフから読み取ってみよう。
相関係数を確認すると、（あ）の0.828が最も強い相関があるね。これは「1試合あたりの得点」と「１試合当たりのショートパスの本数」だね。だからこの選択肢はあっています。
| （２）全参加チームについて正の相関がある組み合わせの中に、決勝進出チームも予選敗退チームも負の相関があるものがある |
さあ（２）だ。この選択肢は、相関の意味が分かっていれば答えられるよね。
全体で「正の相関」があるのに、決勝と予選敗退がともに「負の相関」があるということはありえないでしょう。
よく気づいたね！これは誤りだ。「誤っているものを選べ」だから、答えは（２）だ。
最初から(2)をよく見れば、他の選択肢を検討する必要はなかったんだね。
試験のテクニックとしては、それもありだね。でも、ここではすべての選択肢を確認してみよう
| （３）1試合当たりのショートパス本数の分布を表すグラフ?で、下の段は決勝進出チームのヒストグラムである |
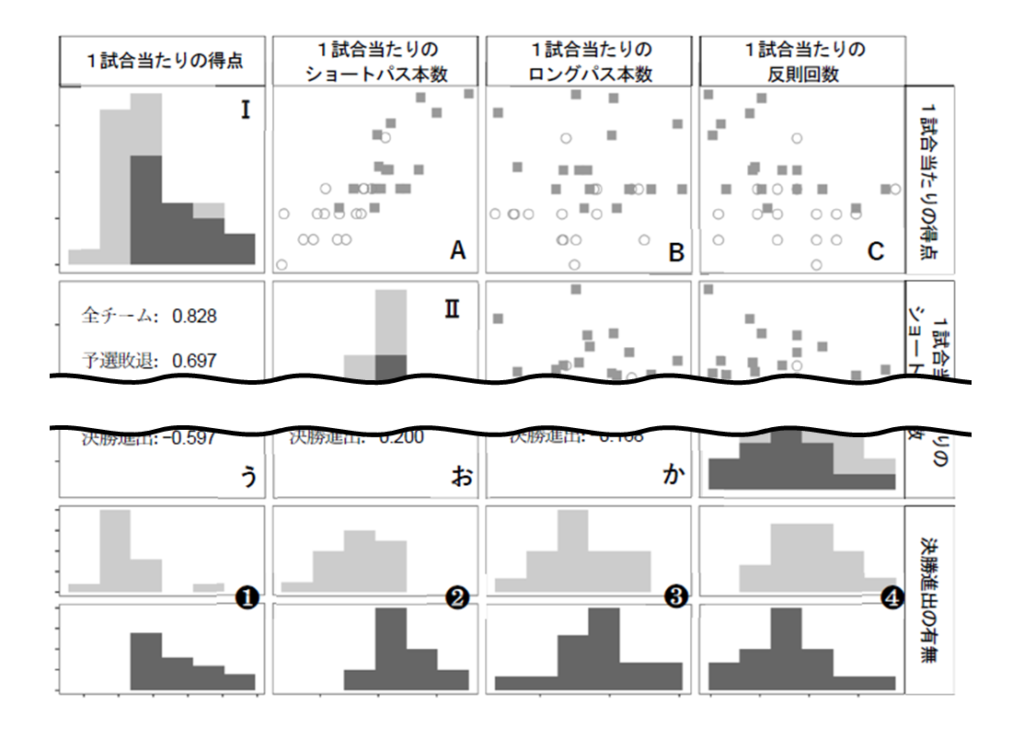
ところで、この表の、Ⅰ～Ⅳや、?～?って、何と何の関係を示しているんですか？
これは複数の項目の関係ではなく、１つの項目について決勝進出したチームと予選敗退したチームを色分けしたものだよ。
むむむ、つまり?は、ショートパスの本数の少なめなチームが上の段、多めの段が下の段だね。ショートパスが多いチームが、決勝進出チームかどうかはわからないな。
そうだね。これは他の項目から推測するしかないね。?つまり「１試合当たりの得点」のグラフからは何が読み取れるだろう？
下のグラフ、つまり黒っぽい色のヒストグラムが、１試合当たりの得点が多いという傾向があるよね。得点が多いチームが決勝進出チームと予想してよさそうだね。
そうだね。だから(3)の選択肢は正解だね。
Jリーグデータを用いたデータ分析実践
今回もGoogle Colaboratoryを使ってグラフを作ってみよう。Google Colaboratoryについては、以前（４５．データの整形と修正）詳しく解説しているので、はじめてのまずそちらから見てね。
はい、今回は何のデータを使って分析するんですか？
２０２３年のJリーグのデータを使ってみよう。Jリーグの公式サイト（https://www.jleague.jp/stats/j1/club/2023/score）から、データを取得してみて。
はい、表示されているデータをJ1league_all_2023.csvに保存しました。ずいぶんいろいろなデータが公開されているんですね。どれを分析しよう。
ここでは、1試合平均得点数、1試合平均パス数、1試合平均スルーパス数、1試合平均ファウル数の値、そして１８チーム中上位９チームか、下位９チームかに分類して結果を分析してみるよ。
面白そう！
散布図・相関行列グラフの表示
import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
# データを読み込む
file_path = 'J1league_all_2023.csv'
data = pd.read_csv(file_path)
# 必要な列（数値データとTop9）を選択
data = data[['1試合平均得点数', '1試合平均パス数', '1試合平均スルーパス数', '1試合平均ファウル数', 'トップ9']]
# 列名を英語に変換
data = data.rename(columns={
'1試合平均得点数': 'Average Goals',
'1試合平均パス数': 'Average Passes',
'1試合平均スルーパス数': 'Average Through Passes',
'1試合平均ファウル数': 'Average Fouls',
'トップ9': 'Top9'
})
# ペアグリッドを作成
g = sns.PairGrid(data, hue="Top9", palette="dark")
# 相関係数を表示する関数
def corrfunc_all(x, y, **kws):
top9_values = data['Top9'].unique()
# 全体の相関係数
corr_values = {'all': np.corrcoef(data[x.name], data[y.name])[0, 1]}
# 各カテゴリーの相関係数
for top9 in top9_values:
subset = data[data['Top9'] == top9]
r = np.corrcoef(subset[x.name], subset[y.name])[0, 1]
corr_values[top9] = r
ax = plt.gca()
# 相関係数を注釈として表示
ax.annotate(f'All: ρ = {corr_values["all"]:.2f}\n'
f'Top9: ρ = {corr_values[1]:.2f}\n'
f'Non-Top9: ρ = {corr_values[0]:.2f}',
xy=(0.5, 0.5), xycoords='axes fraction',
ha='center', va='center', fontsize=10,
bbox=dict(facecolor='white', edgecolor='none', pad=2.0))
# 下三角に相関係数、上三角に散布図、対角線にヒストグラムをマッピング
g.map_lower(corrfunc_all)
g.map_upper(sns.scatterplot)
g.map_diag(sns.histplot)
# 凡例を追加
g.add_legend(title="Top9")
# グラフを表示
plt.show()
じゃあ、Google Colaboratoryを使ってグラフを作ってみよう。
Google Colaboratoryにデータを読みこんで、Pythonのプログラムコードを実行してみます。おっ！出てきました。（リンク）
平均パス数（Average Passes）とスルーパス数（Average Through Passes）の関連性は、どのグラフを見ればよいかな？
相関関係は左から2番目、下から2番目の箱だよね。全体（All）では、Top9チーム（ρ = 0.66）の方が下位９チーム（ρ = 0.32）よりも強い相関を示しているね。
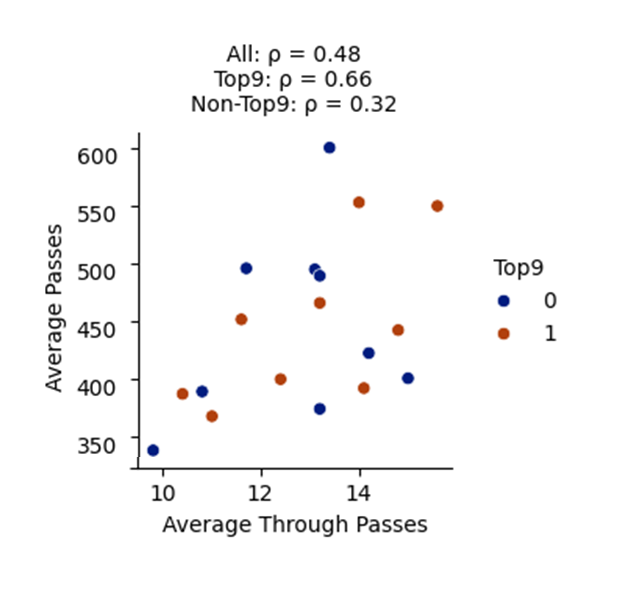
そうだね。上から2番目、左から3番目の相関図を見ても傾向の違いがわかるね。これをどう分析するかな？
上位9チームはパス数が増えるとスルーパスの数も増えている傾向がはっきりしているから、ボールを持つ時間を長く保って、意図的にチャンスを作り出そうとしていると考えられるね。
いいね。
下位9チームは相関が弱いから、パスが増えてもスルーパスの数がそれほど増えないってことかも。彼らはパスを回すことよりも、シンプルにゴールへ向かう戦略を取っている可能性があるね。
ほー、なおや君、サッカーの専門家みたいだね。じゃあ、ファウル（Average Fouls）と相関が強い項目はどれだろう？
ファウル（Average Fouls）とパス数（Average Passes）を示す、一番下で左から2番目の相関係数が気になるね。
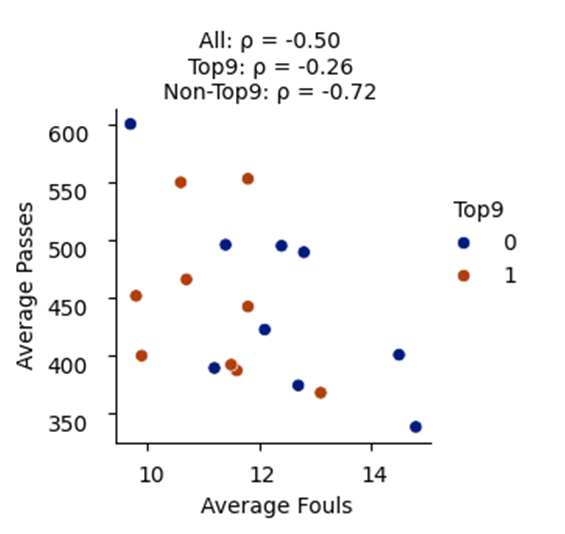
いいところに気が付いたね。全体で-0.50、特に下位9チームでは-0.72と強い負の相関が示されているね。つまり、パス数が多いチームほどファウル数が少ない傾向があるってことだよね。
そう、パスを回してボール保持を重視することで、相手にボールを奪われにくくして、ファウルも少なくなるっていうことだと思うよ。
なるほど。
特に下位チームではその傾向が顕著だから、パスを多くつなぐことでファウルを抑えているんじゃないかな。上位チームは、状況に応じてプレッシャーをかける場面や、ディフェンスで積極的にボールを奪いにいく場面が多いのかもね。
今回は、なおや君が先生みたいだね。データを見ることでいろいろな仮説が立てられるよね。
こんなデータ解析なら毎回でもやりたいな。
いいね。その勢いだ！
まとめ
- 散布図
2つの変数間の関係を視覚的に示すグラフで、正の相関や負の相関を視覚的に確認するのに役立つ。 - 相関係数
変数間の相関の強さを示す指標で、+1に近いほど強い正の相関、-1に近いほど強い負の相関を示す。 - ヒストグラム
データの分布状況を棒グラフで表現し、頻度を示す。 - 相関と因果の違い
相関はデータ間の関連性を示すが、因果は一方の変数が他方に影響を与える関係を指す。 - 散布図・相関行列グラフ
相関係数、散布図、ヒストグラムを1つの図で表現し、変数間の関係性を視覚的に確認できる。
問題
「クイズをスタート」のボタンをクリックすると、５問出題します。さあチャレンジ！
編集者ひとこと
表やグラフの見方が分かれば解ける問題だけれど、理解が追いつくまでに少し時間がかかるかもしれないので、慣れておいたほうが良いですね。
サンプル問題と同じグラフを実際に描いてみたかったのですが。ワールドカップのデータはどこを探しても見つからなかったので、後半ではJリーグの２０２３年のデータを使ってみました。データから得られる考察は、生成系AIに考えてもらったものです。私はサッカーに疎いので、申し訳ないのですが、正しいかどうかは責任持てません。悪しからず。
<RANKING>
高校教育ランキング
