問題文
| 出典:独立行政法人大学入試センター 公開問題「平成30 年告示高等学校学習指導要領に対応した令和7年度大学入学共通テストからの出題教科・科目 情報サンプル問題」 https://www.mext.go.jp/content/20211014-mxt_daigakuc02-000018441_9.pdf |
問3 次の文章を読み,空欄 コ ・ サ に入れるのに最も適当なものを解答群のうちから一つずつ選べ。ただし,空欄 コ ・ サ の順序は問わない。
鈴木さんは,さらに分析を進めるために,データシートを基に,決勝進出チームと予選敗退チームに分けて平均値や四分位数などの基本的な統計量を算出し,表2を作成した。このシートを「分析シート」と呼ぶ。
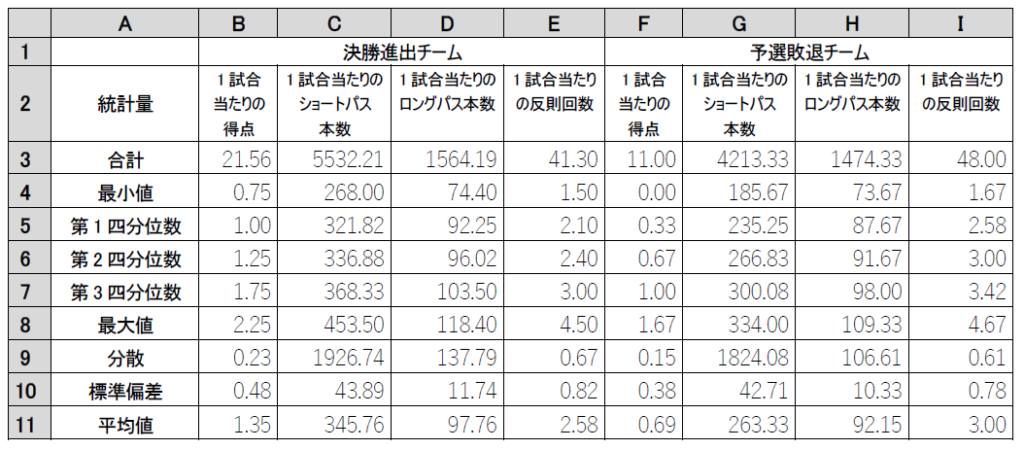
鈴木さんは,この分析シートから(コ) と(サ) について正しいことを確認した。
(コ)、(サ)解答群
| (0)1試合当たりのロングパス本数のデータの散らばりを四分位範囲の視点で見ると,決勝進出チームよりも予選敗退チームの方が小さい。 (1)1試合当たりのショートパス本数は,決勝進出チームと予選敗退チームともに中央値より平均値の方が小さい。 (2)1試合当たりのショートパス本数を見ると,決勝進出チームの第1四分位数は予選敗退チームの中央値より小さい。 (3)1試合当たりの反則回数の標準偏差を比べると,決勝進出チームの方が予選敗退チームよりも散らばりが大きい。 (4)1試合当たりの反則回数の予選敗退チームの第1四分位数は,決勝進出チームの中央値より小さい。 |
解答
- (コ)、(サ)の解答 (0)、(3)(順不同)
解説
本日の授業では、「データの統計的な見方」を学びます。具体的には、データの特徴を示す指標である四分位範囲、中央値と平均値の違い、標準偏差、分散について学びます。また、これらを視覚的に表現する箱ひげ図の読み方や活用方法についても詳しく解説します。データ分析をより深く理解するための基礎的な考え方を身につけましょう。
黒板
統計量の意味

なおや君、まずこの表2の見方について復習してみようか。各種の統計量の意味は分かるかな?

うーん、最小値や最大値は分かるんですけど、四分位数って、データを4つに分けるってことで合ってます?

その通り!四分位数はデータを小さい順に並べて、全体を4つの区切りに分けたときの位置にある値なんだ。

なるほど、第1四分位数はデータを小さい順に並べたとき、下から4分の1の位置にくるデータ、第2四分位数は真ん中(半分)の位置、第3四分位数は下から4分の3の位置にくるデータということですね。

その通り!さらに、第1四分位数と第3四分位数の間にはデータ全体の50%が含まれるんだよ。ちなみに、第2四分位数は「中央値」とも呼ばれるんだ。
分散と標準偏差

次は分散と標準偏差に進もう。分散について知ってるかな?

確か、データのバラつきを示す値ですよね?

その通り。分散は、「各データと平均値との差の平方(2乗)の平均値」だ。


なんでわざわざ差の2乗とかを使うんですか?

いい質問だね!2乗することによって、マイナスの差があっても値が打ち消されないから、バラつきを正しく捉えられるんだよ。

なるほど、だから2乗してるんですね!でも、標準偏差は何のために使うんですか?

標準偏差は分散の平方根を取ったものなんだ。分散のままだと値が大きすぎるから、元のデータのスケールに戻すために平方根を取るんだよ。
統計量の計算(合計、最小値、四分位数、最大値)

では、実際に、10個のデータ「53, 48, 62, 49, 44, 45, 52, 34, 51, 70」を使って統計値を計算してみよう。まず、合計と最小値、最大値を計算してみて。

はい。合計は53 + 48 + 62 + 49 + 44 + 45 + 52 + 34 + 51 + 70 = 508ですね。最小値は34、最大値は70です!

その通り!では次に四分位数を計算しよう。まず、データを小さい順に並べるところから始めようか。

データを小さい順に並べると「34, 44, 45, 48, 49, 51, 52, 53, 62, 70」ですね。中央値(第2四分位数)は真ん中といっても、5番目と6番目のどちらを使えばよいんだろう?

ちょうど真ん中の数がない場合は、それを挟む2つの数の平均をとろう。今回は、真ん中の2つ、49と51の平均だから(49 + 51) ÷ 2 = 50だよ。次に第1四分位数と第3四分位数を求めてみようか。

第1四分位数は前半「34, 44, 45, 48, 49」の中央値で45です。第3四分位数は後半「51, 52, 53, 62, 70」の中央値で53ですね!
統計量の計算(平均値、分散、標準偏差)

じゃあ、次に平均値を計算してみようか。データ全体の傾向が分かる指標だよ。

合計が514でデータ数が10なので、平均値は514 ÷ 10 = 51.4ですね!

最後に分散と標準偏差を計算してみよう。まず、各データと平均値との差を求めてて、それを2乗してみて。

頑張って、次のように計算しました。


お疲れ様。これらの値を合計すると、873.6になるね。分散はこれをデータ数10で割ったものだから、87.36になるね。

標準偏差はこの平方根なので、9.349ですね!
データ:53, 48, 62, 49, 44, 45, 52, 34, 51, 70 の統計量
| 合計 | 508 |
| 最小値 | 34 |
| 第1四分位数 | 45 |
| 第2四分位数(中央値) | 50 |
| 第3四分位数 | 53 |
| 最大値 | 70 |
| 分散 | 87.36 |
| 標準偏差 | 9.349 |
| 平均値 | 50.8 |
箱ひげ図による四分位数の可視化

四分位数を視覚的にわかりやすく表現する方法として、箱ひげ図があるよ。

箱ひげ?

箱ひげ図は、データのばらつきや分布を一目で理解できるグラフなんだ。箱の部分が四分位範囲を示していて、ひげの部分が最小値と最大値を表しているんだよ。

なるほど。箱の中が第1四分位数から第3四分位数で、真ん中にある線が中央値ということですね。

その通り!これを使うと、データがどの範囲に集中しているかや、外れ値があるかどうかが直感的にわかるんだ。サッカーのチームごとに得点やパス数を箱ひげ図で比較すると違いがよく見えるよ。表2のデータを箱ひげ図で描いたので見てみて。

たしかに、さっきのデータで上位チームと下位チームの特徴がすぐに分かりそうですね!

選択肢(0) の確認
| (0)四分位範囲 試合当たりのロングパス本数のデータの散らばりを四分位範囲の視点で見ると、決勝進出チームより予選敗退チームの方が小さい |

では、(0)を見ておこう。

四分位範囲って、何でしょう?さっき教えてもらった、第1から第3の四分位数と関係あるんですか?

いいところに気が付いたね。四分位範囲というのは第3四分位数と第1四分位数の差の事だ。

なるほど、じゃあ、第3四分位数から第1四分位数を引けばいいんですね。

その通り、決勝進出チームと、予選敗退チームのそれぞれで計算してみよう。

計算すると次の通りですね。

決勝進出チームの方が、予選敗退チームの方が小さいので、これは正しい選択肢ですね。

良いね!
選択肢(1)の確認
| (1)1試合当たりのショートパス本数は、決勝進出チームと予選敗退チームともに中央値より平均値の方が小さい |

次に(1)の選択肢を見てみよう。「ショートパス本数は、どちらのチームも中央値より平均値の方が小さい」とあるけど、どうだろうね?

中央値って第2四分位数でしたよね。表のデータを見ると、決勝進出チームは中央値が336.86本で、平均値が345.76本。予選敗退チームは中央値が266.83本で、平均値が263.33本です。

そうだね。この結果から分かることは?

決勝進出チームでは平均値の方が大きいです。一方で、予選敗退チームは中央値の方が大きいので、この選択肢は正しくありませんね!

その通り!選択肢の条件が満たされていないから、不正解だね。次に進もうか。
選択肢(2)の確認
| (2)1試合当たりのショートパス本数を見ると、決勝進出チームの第1四分位数は予選敗退チームの中央値より小さい |

(2)では「決勝進出チームの第1四分位数が予選敗退チームの中央値より小さい」とあるけど、どうだろうね?

えーっと、決勝進出チームの第1四分位数は306.63本、予選敗退チームの中央値は266.83本ですね。比べてみると、明らかに決勝進出チームの第1四分位数の方が大きいですね。

その通り!この条件も成り立たないから、不正解となるね。しっかり確認できていて素晴らしいよ。
選択肢(3)の確認
| (3)1試合当たりの反則回数の標準偏差を比べると、決勝進出チームの方が予選敗退チームよりも散らばりが大きい |

(3)について見てみようか。「反則回数の標準偏差を比べる」とあるけど、標準偏差の値はどうなっている?

決勝進出チームの標準偏差は0.82、予選敗退チームは0.78ですね。なので、決勝進出チームの方が少しだけ散らばりが大きいですね。

その通りだね!これは条件を満たしているから、正しい選択肢だね。簡単だったかな?

はい、ここはすぐに分かりました!
選択肢(4)の確認
| (4)1試合当たりの反則回数の予選敗退チームの第1四分位数は、決勝進出チームの中央値より小さい |

最後に(4)を確認しよう。

まず、予選敗退チームの第1四分位数が2.50で、決勝進出チームの中央値が2.10ですね。予選敗退チームの方が大きいので、この選択肢も不正解です。

完璧だね!これで全ての選択肢を確認できたよ。どうだった?

全体的に比較する視点が分かりやすくなりました。間違いのある選択肢でも、どうして誤りなのかを考えるのが面白かったです!
実データを用いた確認
統計量データの準備

今回もGoogle Colaboratoryを使ってグラフを作ってみよう。Google Colaboratoryについては、以前(45.データの整形と修正)で詳しく解説しているから、初めて使う場合はそちらを確認してみてね。

はい、今回は何のデータを使って分析するんですか?

前回と同じく、2023年のJリーグのデータを使って箱ひげ図を作成してみよう。データの入手先や概要は3-1の授業資料にまとめてあるから、それも参考にしてね。

あれ?でもこのデータには平均値とか、第1四分位数などの統計値は入っていませんよね?

そうだね。だから、まずは統計値を計算した表を作る必要があるんだ。上位9チームと下位9チームに分けて計算してみたよ(データ)

どうやってこんな計算ができるんですか?エクセルとかですか?

そうだよ。表計算ソフトを使えば簡単にできるんだ。今回は授業の目的とは少し違うから詳しくは省略するけど、また別の機会に説明するよ。

了解しました。今度ぜひ教えてください!
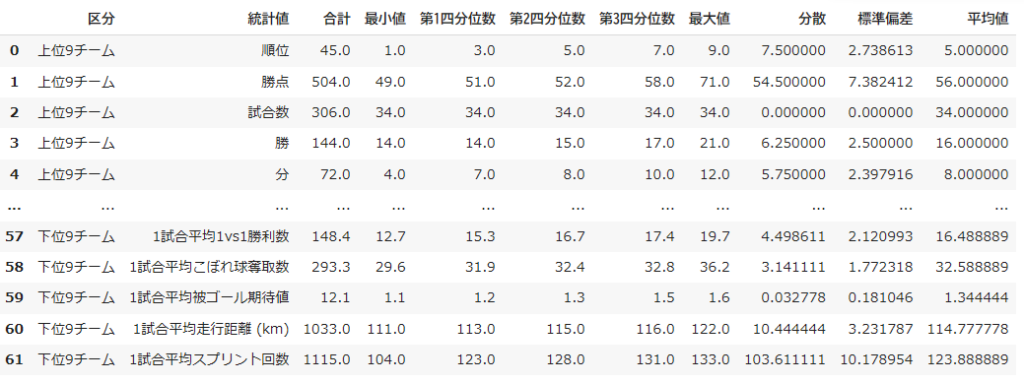
箱ひげ図の作成
import pandas as pd
import matplotlib.pyplot as plt
# CSVファイルを読み込む
data = pd.read_csv('J12023_boxplots.csv')
# 「上位9チーム」と「下位9チーム」のデータをフィルタリング
top9_data = data[data['区分'] == '上位9チーム']
bottom9_data = data[data['区分'] == '下位9チーム']
# 統計値のリストを取得
statistics = data['統計値'].unique()
# 統計値の英語翻訳ラベル(適宜文脈に応じて置き換えてください)
stat_labels = [
"Ranking", "Points", "Matches", "Wins", "Draws", "Losses",
"Goals", "Conceded Goals", "Goal Difference", "Shots per Game",
"Shots Conceded per Game", "On-Target Shots per Game",
"On-Target Shots Conceded per Game", "Goals per Game",
"Goals Conceded per Game", "Passes per Game", "Dribbles per Game",
"Through Passes per Game", "Crosses per Game", "Clearances per Game",
"Tackles per Game", "Blocks per Game", "Fouls per Game",
"Interceptions per Game", "Aerial Duels Won per Game",
"Chances Created per Game", "1v1 Wins per Game",
"Loose Ball Recoveries per Game", "Expected Goals Conceded per Game",
"Distance Covered (km) per Game", "Sprints per Game"
]
# "per Game" を含む項目のみをフィルタ
filtered_stats = [
(stat, label) for stat, label in zip(statistics, stat_labels) if "per Game" in label
]
# 10x3のグリッドを作成して箱ひげ図を描画
fig, axes = plt.subplots(10, 3, figsize=(18, 30))
axes = axes.flatten()
# 各統計値についてループして箱ひげ図を作成
for i, (stat, label) in enumerate(filtered_stats):
if i < len(axes): # プロット数が利用可能な軸数に収まるか確認
# 上位9チームと下位9チームのデータを取得
top9_values = top9_data[top9_data['統計値'] == stat][['最小値', '第1四分位数', '第2四分位数', '第3四分位数', '最大値']].values.flatten()
bottom9_values = bottom9_data[bottom9_data['統計値'] == stat][['最小値', '第1四分位数', '第2四分位数', '第3四分位数', '最大値']].values.flatten()
# 箱ひげ図を描画し、指定された色を適用
bplot = axes[i].boxplot(
[top9_values, bottom9_values],
labels=['Top 9', 'Bottom 9'],
patch_artist=True,
medianprops=dict(color='white') # 中央値のラインを白色に設定
)
bplot['boxes'][0].set_facecolor('blue') # 上位9チームを青で表示
bplot['boxes'][1].set_facecolor('red') # 下位9チームを赤で表示
# 箱ひげ図の横に数値ラベルを追加
for j, values in enumerate([top9_values, bottom9_values]):
x_pos = j + 1.2 # 箱の右横に配置
for k, value in enumerate(values):
y_pos = value
axes[i].text(x_pos, y_pos, f"{value:.2f}", fontsize=8, va='center')
# タイトルと軸ラベルの設定
axes[i].set_title(label, fontsize=10)
axes[i].tick_params(axis='x', rotation=45)
# 使われていないサブプロットを非表示
for j in range(i + 1, len(axes)):
axes[j].axis('off')
# 全体のタイトルとレイアウト調整
fig.suptitle("Comparison of Metrics 'per Game' for Top 9 and Bottom 9 Teams", fontsize=16)
fig.tight_layout(rect=[0, 0, 1, 0.97])
plt.show()
それじゃあ、Google Colaboratoryを使って実際にグラフを作成してみよう。リンク先はココだよ

Google Colaboratoryにデータを読み込んで、Pythonのコードを実行します。おっ!いっぱいグラフが出てきました!
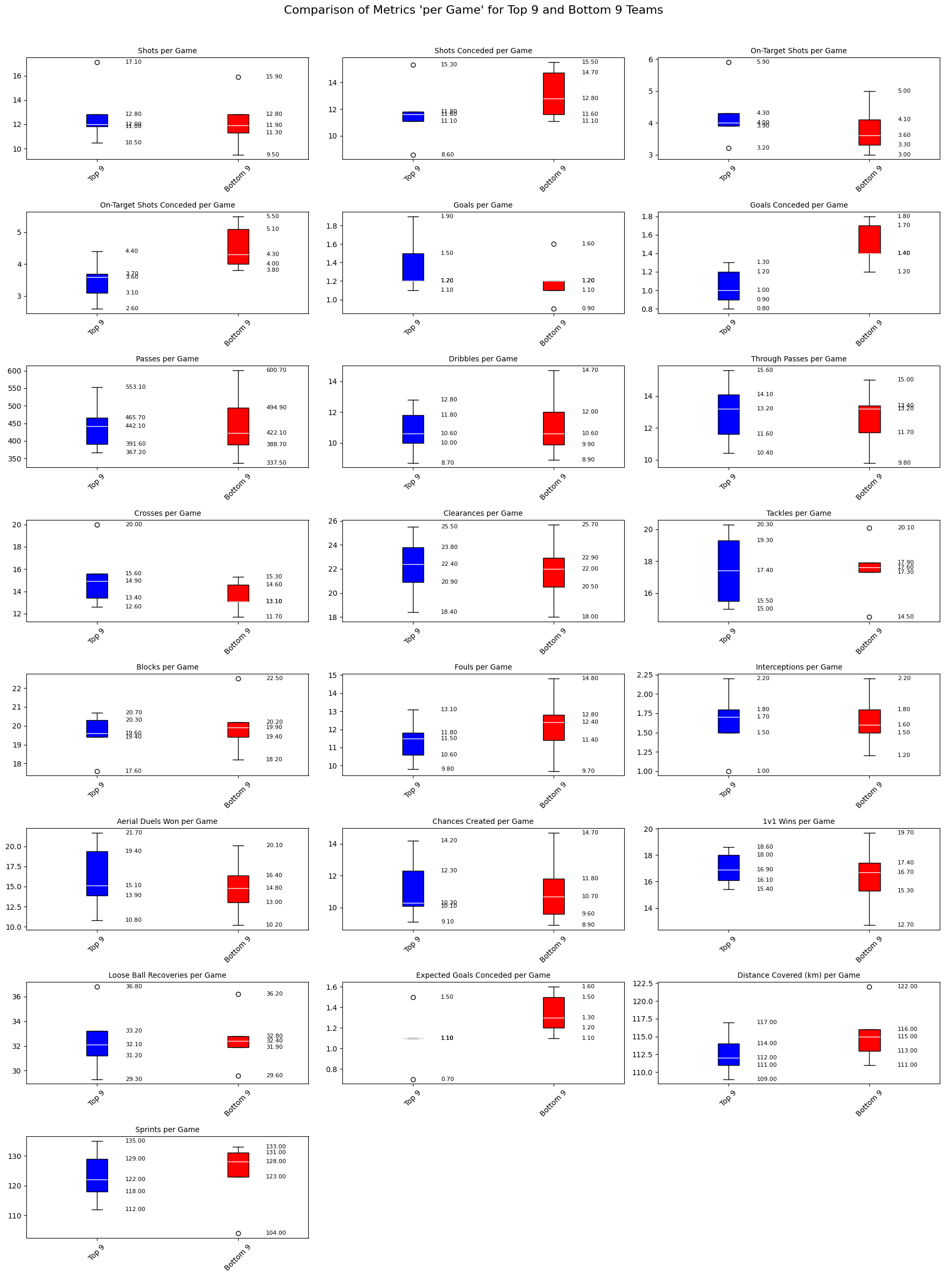
四分位数と箱ひげ図を用いたデータ分析
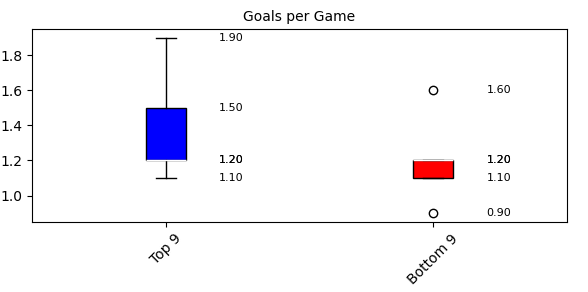

1試合当たりのゴール数(Goals per Game)を見ると、上位チームの第3四分位数が1.5点なのに対して、下位チームは1.2点にとどまっているね。この差は、得点力の違いを表しているんじゃないかな?

そうですね。上位チームは得点できる場面をしっかりとものにしている証拠だと思います。一方、下位チームは攻撃のバリエーションが少ないか、決定力が低いことが課題だと考えられますね。
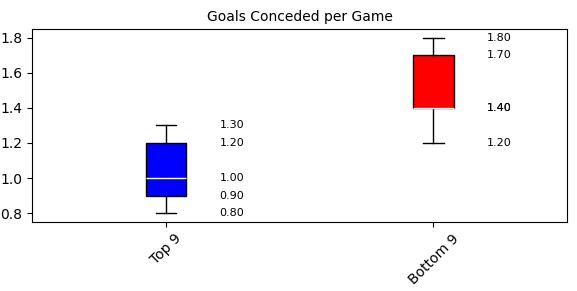

失点数を見ると、上位チームの中央値が1.0点なのに対して、下位チームは1.4点と差が出ているね。特に第3四分位数では、上位チームが1.2点、下位チームは1.7点と守備力に違いがあるのが分かるね。

はい。上位チームは守備が組織的で安定しているので、大量失点する試合が少ないのだと思います。逆に下位チームは、個々の守備力や連携に問題がある可能性がありますね。
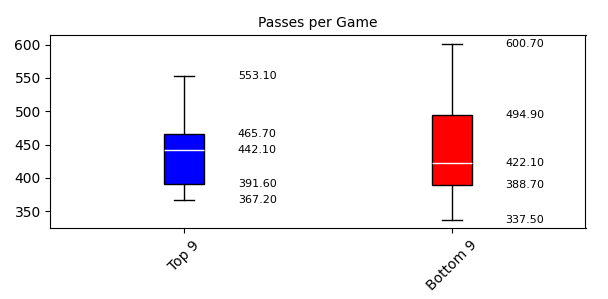

パス数に注目すると、上位チームの442.1は下位チーム422.1よりも高く、全体的にパス数が多い傾向があるね。でも上位チームの第3四分位数は465.7本ですが、下位チームでは494.9本と少し多くなっているね。これは一見、下位チームが優れているようにも見えるけど、どう解釈すればいいのかな?

上位チームはパス戦術が安定しているのに対し、下位チームはばらつきが大きく、試合ごとにパフォーマンスが不安定なのかもしれませんね。
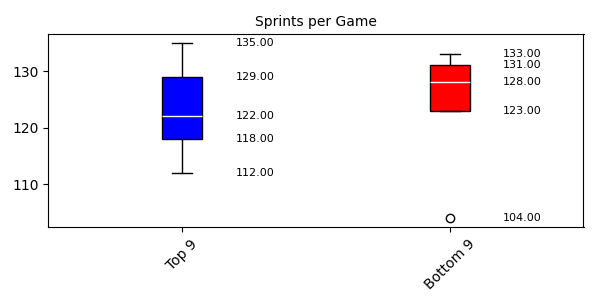

スプリント回数では、上位チームの第1四分位数が118回、下位チームが123回と差があるね。でも、第3四分位数では上位チームが129回、下位チームが131回と接近している。これについてはどう見えるかな?

上位チームは選手全体でバランス良くスプリントしているのに対し、下位チームは特定の選手に負担が偏っている可能性があります。運動量が均一でないと、守備や攻撃の連携が崩れやすいです。
授業のまとめ

まとめると、上位チームは得点力や守備の安定性、パス戦術、運動量の統一性が強みだと言えそうだね。一方で、下位チームは戦術やパフォーマンスのばらつきが課題になっているようだ。今日は良い分析ができたね!

ありがとうございます!データを視覚的に分析する方法がとても面白かったです。次の試合を見るときの楽しみが増えました!
まとめ
- 四分位範囲
四分位範囲とは、データのばらつきを示す指標で、第1四分位数と第3四分位数の差を指す。データの中心50%がどの範囲に集中しているかを表す。 - 中央値と平均値の違い
中央値はデータを小さい順に並べた際の真ん中の値で、外れ値の影響を受けにくい。一方、平均値はデータの総和をデータ数で割った値で、外れ値に敏感に反応する。 - 分散
分散は、各データと平均値との差を2乗して平均した値で、データのばらつきを数値化したもの。2乗することで、プラスとマイナスの差が打ち消し合わないようにしている。 - 標準偏差
標準偏差とは、データが平均値を中心にどれだけ散らばっているかを示す指標で、分散の平方根を取った値。 - 箱ひげ図
箱ひげ図とは、データの分布を視覚的に表すグラフで、中央値、四分位範囲、最小値、最大値、外れ値を一目で確認できる。データのばらつきや分布の特徴を理解するために用いられる。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジ!
関連授業
編集者ひとこと
今回の問題は、四分位の意味が分かっていれば、比較的簡単に答えられる問題でした。
それでは物足りないので、箱ひげ図を使った解説を試してみましたが、いかがでしょうか?
J1リーグの各種統計データを、Google Colaboratorが表示してくれた時はちょっとした感動ものでした。データ分析の世界を堪能してくださいね。
<RANKING>![]()
高校教育ランキング



