問題文
| 出典:独立行政法人大学入試センター 公開問題「平成30 年告示高等学校学習指導要領に対応した令和7年度大学入学共通テストからの出題教科・科目 情報サンプル問題」 https://www.mext.go.jp/content/20211014-mxt_daigakuc02-000018441_9.pdf |
問4 次の文章を読み,空欄 (シ)に入れる最も適当なものを解答群のうちから一つ選べ。
また,(ス) ・(セソ) については,当てはまる数字をマークせよ。
鈴木さんは,作成した図1と表2の両方から, シ ことに気づき,決勝進出の有無と1試合当たりの反則回数の関係に着目した。そこで,全参加チームにおける1試合当たりの反則回数の第1四分位数(Q1)未満のもの,第3四分位数(Q3)を超えるもの,Q1 以上Q3 以下の範囲のものの三つに分け,それと決勝進出の有無で,次の表3のクロス集計表に全参加チームを分類した。ただし,※の箇所は値を隠してある
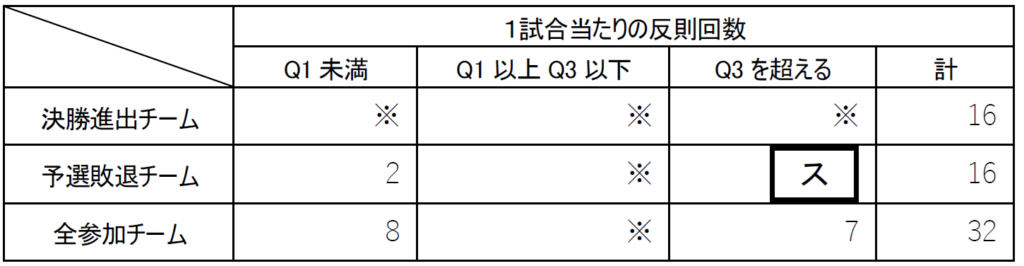
この表から,決勝進出チームと予選敗退チームの傾向が異なることに気づいた鈴木さんは,割合に着目してみようと考えた。決勝進出チームのうち1試合当たりの反則回数が全参加チームにおける第3四分位数を超えるチームの割合は約19%であった。また,1試合当たりの反則回数がその第1四分位数より小さいチームの中で決勝進出したチームの割合は (セソ)%であった。
その後,鈴木さんはこの分析の結果を顧問の先生に相談し,部活動のメンバーにも報告した。そして,分析の結果を参考にしてサッカー部の今後の練習計画と目標を再設定するとともに,さらなる知見が得られないか分析を進めることとした。
(シ)解答群
| (0)1試合当たりの反則回数が最も多いチームは,決勝進出チームである (1)1試合当たりの反則回数と1試合当たりの得点の間には,全参加チームにおいて正の相関がある (2)1試合当たりの反則回数と1試合当たりの得点の間には,決勝進出チームと予選敗退チームのそれぞれで負の相関がある (3)図1の(4)のヒストグラムでは決勝進出チームの方が予選敗退チームより分布が左にずれている |
解答
- (シ)の解答 (3)
- (ス)の解答 (4)
- (セソ)の解答 75
解説
今日の授業では、クロス集計表とグラフを使ってデータ分析を行います。また、エクセルを用いたクロス集計表の作成とグラフによる可視化の方法も説明します。
黒板
クロス集計表の読み解き(設問シ)
| 鈴木さんは、作成した図1と表2の両方から、(シ)ことに気づき・・・ |

いよいよ分析ですね!どれが正しいのか考えるのが楽しみです!

じゃあ、選択肢(0)からいこう。「1試合当たりの反則回数が最も多いチームは、決勝進出チームである」ってあるけど、Cグラフの右端に注目してみて
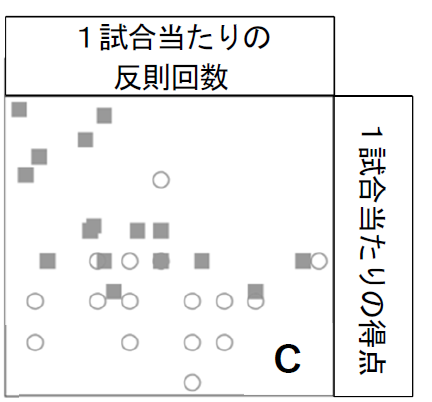

確かに、右端には〇がありますね。〇は、予選敗退チームのデータでしたね。だから、この選択肢は誤りですね

その通り!じゃあ次は選択肢(1)。「1試合当たりの反則回数と1試合当たりの得点の間には、全参加チームにおいて正の相関がある」だ。「う」の相関係数を見てどう思う?


全チームの相関係数は-0.398だから負の相関ですね!正の相関なんて言えません。これも誤りですね

よくできたね!次は選択肢(2)。「決勝進出チームと予選敗退チームのそれぞれで負の相関がある」だ。どうかな?

これ「う」から読み取れますね。予選敗退チームは0.047で無相関に近いです。これも誤りですね

じゃあ最後の選択肢(3)。「図1の(4)のヒストグラムでは決勝進出チームの方が予選敗退チームより分布が左にずれている」だよ。どうだい?
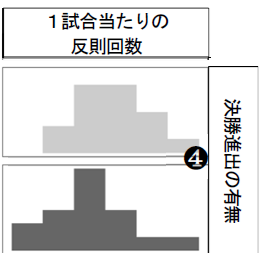

下の段の濃い灰色が決勝進出チームでしたね。下の段の方が、上の段の予選敗退チームより左側に分布しています。だから、これが正解ですね!

その通り!だから(シ)の解答は(3)だね。よくできました!

改めて、解答群を見ると、決勝進出チームの方が反則が少ないことが分かっていれば、(3)以外は明らかに変でしたね。

良いね。そういう感覚になれば、データ分析のセンスが付いてきた証拠だね。でも、データをしっかり確認して裏を取ることも重要だ。
クロス集計表の穴埋め(設問(ス))
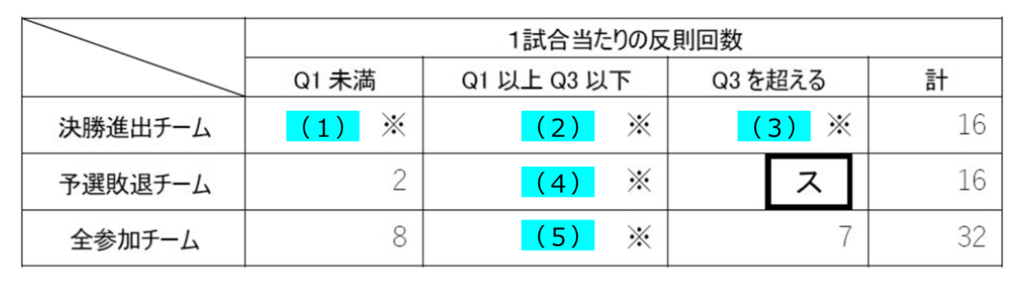

まず、表3の※のところに、番号を振ってみたよ。(ス)を求めるには、どこに注目すればよいかな?

うーん、この表どうやって見ればよいんですか?

クロス集計表とは、データを集計する時に、2つ以上の観点でまとめる統計手法のことだ。表の上部の「表頭(ひょうとう)」、表の左側の「表側(ひょうそく)」で構成されるよ。

なるほどね。ところでこの「Q1未満」とか書かれていますけれど、この「Q」って何ですか?

四分位数 (quartile points)を「Q」と略すんだ。第1四分位はQ1、第2四分位はQ2、第3四分位はQ3だよ。

これで表の見方はわかりました。でもどうやってこの問題を解けばよいのか見当もつきません。

最後の行や列は合計値だよ。それをヒントに(ス)の値を考えて。

なるほど、「Q3を超えると書かれた列」に注目すると、(3)+(ス)=7ですね。

良いね。行に注目するとどうかな?

「予選敗退チーム」の行に注目すると、2+(4)+(ス)=16ですね。うーん、(4)の値がわからないと、解けないですね

そうだね。(3)か(4)の値が、設問中のどこかにあるから探してみて。

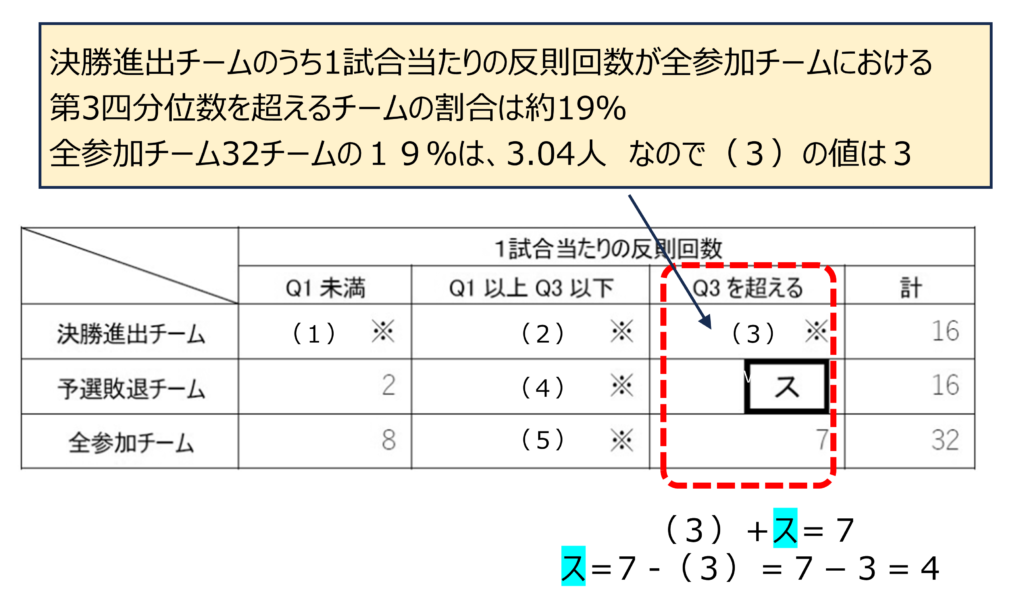
「決勝進出チームのうち1試合当たりの反則回数が全参加チームにおける第3四分位数を超えるチームの割合は約19%であった。」が(3)の事を言ってそうですね。

素晴らしい。じゃあ19%というのは、何チームの事かな?

決勝進出チームは16チームだから、これを掛ければいいんですね?

その通り!計算すると、「16 × 19 ÷ 100 = 3.04」になる。これを四捨五入して、(3)は「3」だね。

(3)+(ス)=7で、(3)が3ということなら、(ス)の値は4ですね。

その通り!設問からヒントを読み解けたのが正解の秘訣だったね。
クロス集計表の穴埋め(設問(セソ))
| 1試合当たりの反則回数がその第1四分位数より小さいチームの中で決勝進出したチームの割合はセソ%であった。 |

この設問で聞いているのは、表の中のどの値だろう?

「第1四分位数より小さいチーム」というのは一番左の「Q1未満」ですね。そして「決勝進出したチーム」は一番上の行だから、先ほど番号を付けた(1)のところの値ですね。

良いね。ではこのあたりはいくつかな?

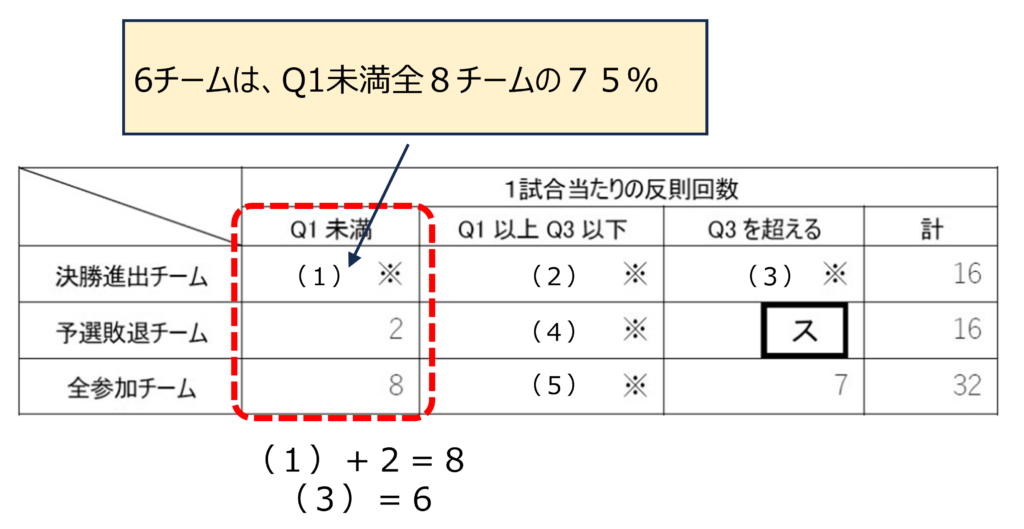
「Q1未満」の列を見ると、(1)+2=8ですから。(1)は6ですね。

さすが!表の見方は完璧だね。では6チームというのはQ1未満の全チームの内何パーセントかな?

Q1未満の8チームの中の6チームだから、75%ですね。

完璧!
実データを用いた確認(エクセルを用いたクロス集計表作成)

本日の授業では、マイクロソフト エクセルを使用して「J1リーグ2023年の1試合平均ファウル数」を分析してみよう。

エクセルは学校でも使ったことがありますが、関数とか複雑でよくわかりません。

今回は一つ一つ解説しながら進めるから安心して。
(1)使用するデータと、セル範囲の名前付け

今回利用するデータはJ1リーグ 2023年1試合平均ファウル数のデータだ(J1league_faul_Cross_2023_org.xlsx)。これまでも利用してきたデータだよ。詳しくは3-1の授業資料を参考にしてね。(※:本ファイルはExcel2007以降のバージョンに対応しています)
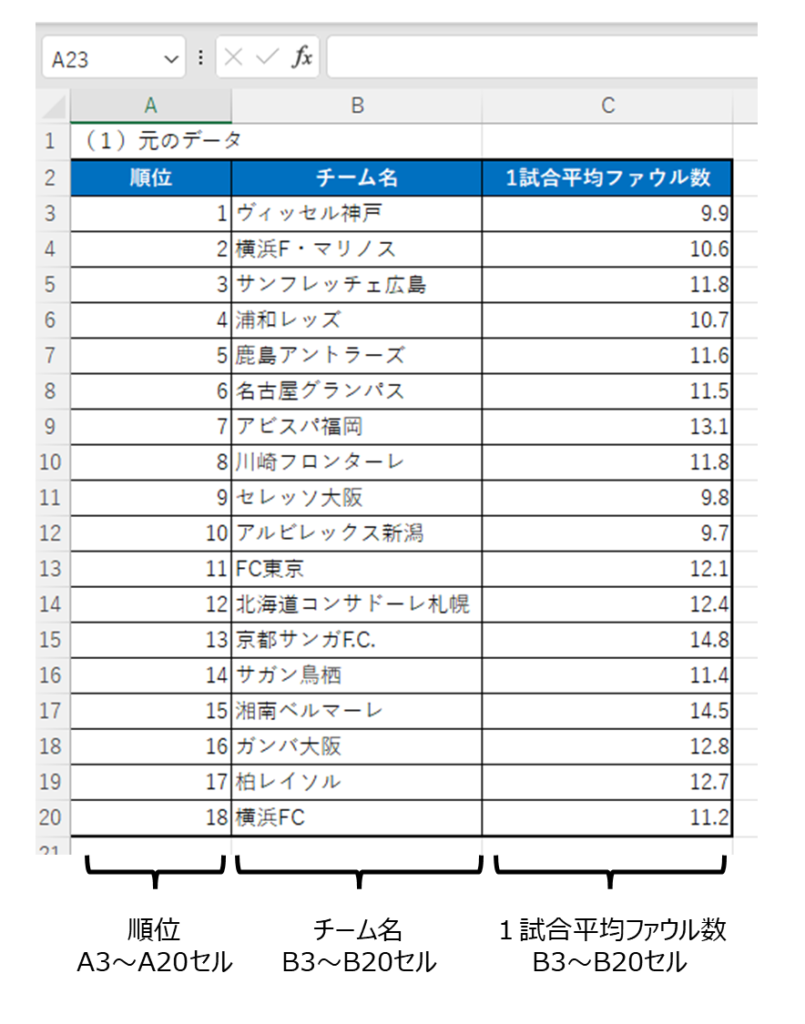

おなじみのデータですね。

データの分析を効率よくするには、セル範囲に名前を付けるのが便利だよ

セル範囲に名前を付けられるんですか?知らなかった…

例えば、順位がA3セルからA20セルにあるとしたら、それを選択して名前ボックスに「順位」と入力してEnterキーを押すだけでいいんだ


名前を付けると何が楽になるんですか

関数で計算するときにセル範囲を直接参照するよりも分かりやすくなるし、後から見返すときも便利だよ

では、C3セルからC20セルは、「ファウル数」という名前を付けます。
(2)四分位数の計算

では、このデータを基に四分位数を計算するよ。今回は第1四分位数と、第2四分位数を求めよう。

はい。四分位数についてはばっちりです。でもエクセルではどうやって計算するのかさっぱりわかりません

四分位数を求めるには、「QUARTILE.EXC」という関数を使うよ。

何か難しそうな名前の関数ですね。

名前はちょっと難しそうな雰囲気だけれども、使い方は簡単だよ。かっこの中の最初の引数にデータの範囲を指定して、2つ目の引数に1とか3とかを入れればよいんだ。
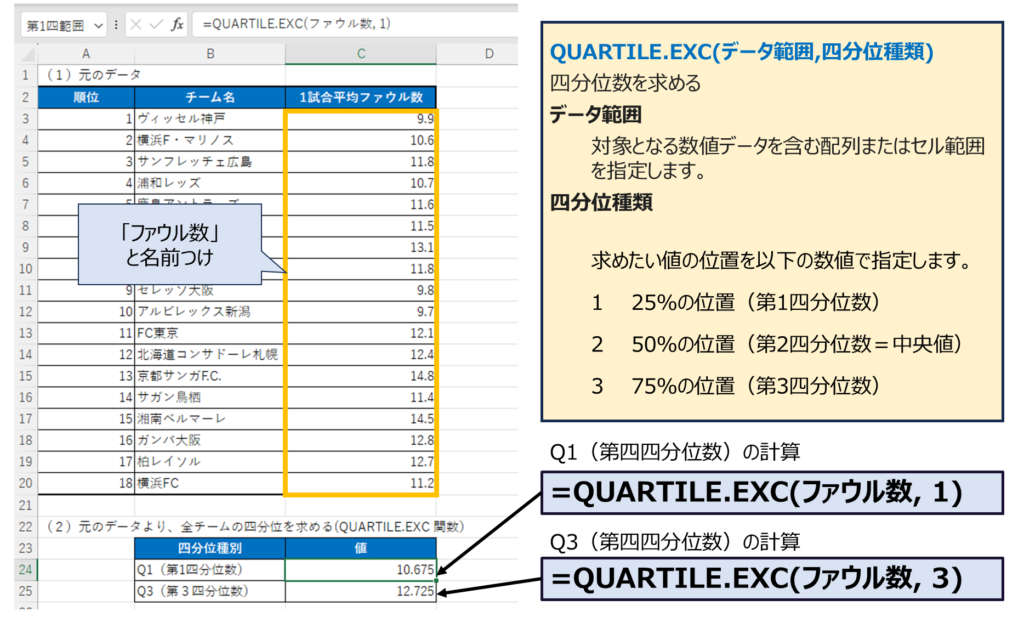

もしかして、その1というのは第1四分位数の意味ですか?

するどい!1を指定すると、第1四分位数、2を指定すると第2四分位数つまり中央値、3を指定すると第3四分位数が求められるんだ。

なるほど。計算すると第1四分位数は10.675、第2四分位数は12.725ですね。
(3)箱ひげ図の作成

せっかくだから、箱ひげ図を使ってデータを視覚化してみよう

エクセルで箱ひげ図も描けるんですか?

データを選択して、[挿入]タブの[統計グラフの挿入]から[箱ひげ図]を選ぶだけで作成できるんだ
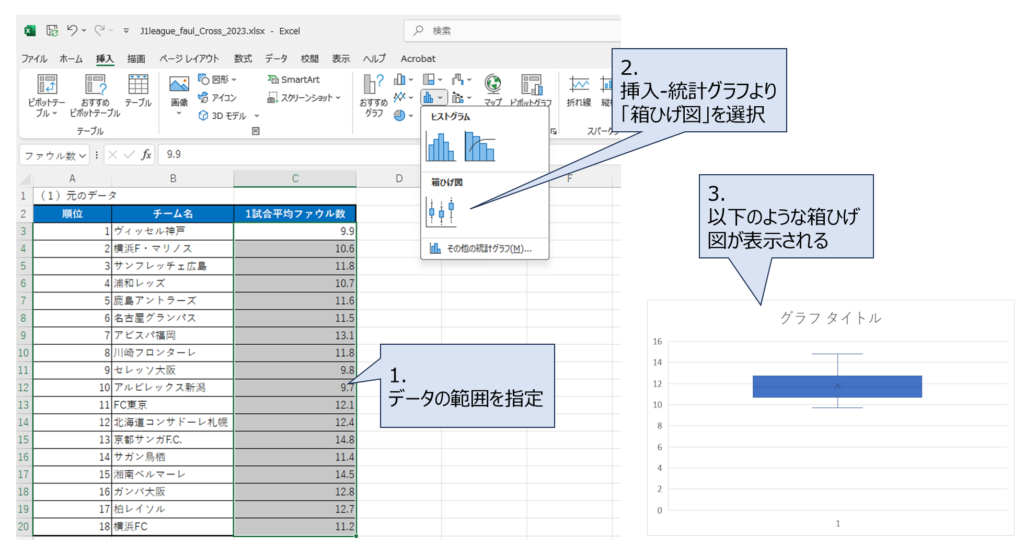

本当だ。でもこのグラフはタイトルとか何も入っていなくてさみしいですね。

そうだね。グラフ要素として、軸、タイトル、データラベル、メモリ線を追加するのがおすすめだよ
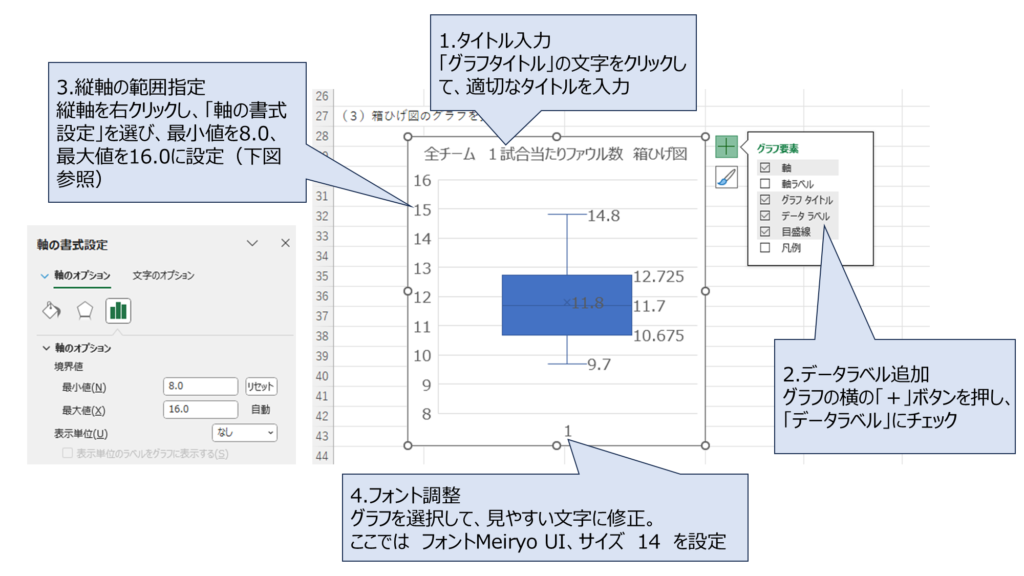
(4)四分位範囲の判定(IF関数の活用)

次はIF関数を使って、各チームのデータがどの四分位に属するかを判定する方法をやってみよう

エクセルで、IF関数は使ったことがありますが、ちゃんと使えるかどうかは・・

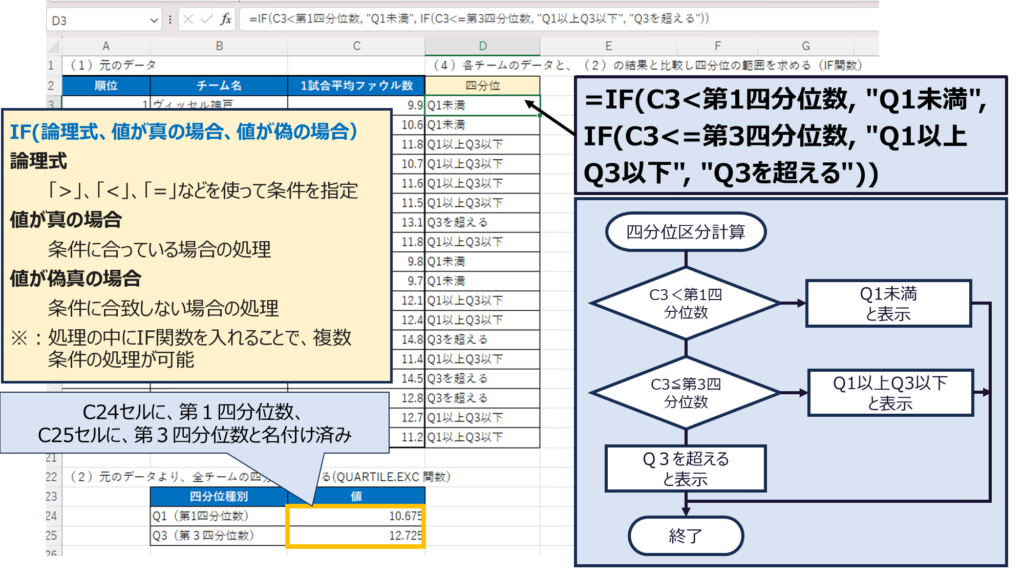
IF関数は一番よく使われる関数だから、しっかり理解しておこう。IF(論理式、値が真の場合、値が偽の場合)というシンプルな式だよ。

そうそう、これです。

条件が一つだと単純だけど、複数しているする場合は、IF(論理式、値が真の場合、IF(論理式、値が真の場合、値が偽の場合))というような書き方もできるんだ。

ん?今の例では、「値が偽の場合」とのころに、さらにIF文が入れ子で入っているといこと?

その通り!こうやって入れ子で記述することで、条件を複数設定できるんだ。今回はまず第1四分位数より小さいか比較、次に第3四分位より小さいか比較と2段階に比較することで、3つの区分に分けているよ。

なるほど、よーく見るとそれほど難しくはないですね
(5)クロス集計表

いよいよクロス集計表の作成だ。クロス表では、順位(上位9 or 下位9)×四分位数の範囲(Q1未満 or Q1以上Q3以下or Q3を超える)という6マスを埋めよう

順位と、四分位の両方が入った表から、条件の合ったチーム数をカウントする必要がありますね。関数を考えるより、目で見て数えたほうが簡単じゃないですか?

これくらいの数なら、確かにその通りだね。でも今回はエクセルの関数を作ってみよう。一度関数ができてしまえば、何千チームあっても一発で計算できるからね。

はい。頑張ります。

今回は、COUNTIFS関数を使うよ。複数の範囲のセルに条件を適用して、すべての条件が満たされた回数をカウントする関数だよ。

そういわれても・・。具体的にどう使うか教えてください。

そうだね。ではクロス集計表の「Q1未満」×「上位9チーム」のセルに入れる関数を考えてみよう。

はい、一番左上の箱ですね。

ここには、=COUNTIFS(順位,”<=9″,四分位,”Q1未満”)を入れるんだ。「順位,”<=9″」までが1つ目の条件、「四分位,”Q1未満”」が2つ目の条件で、この2つの条件をすべて満たしたチームの数を数えるんだ。
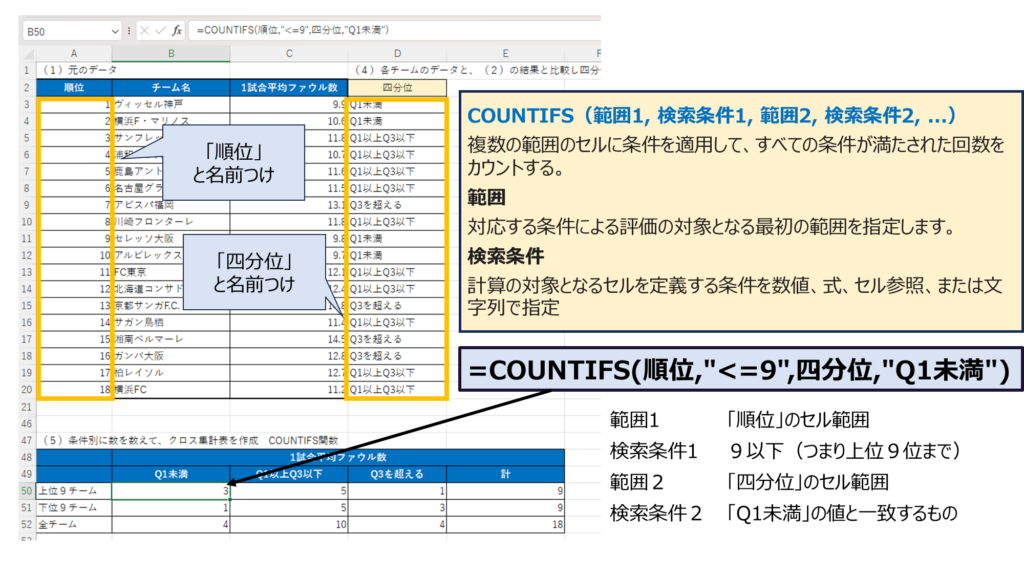

なるほど、一つ目が順位の値が9以下という条件、2つめが四分位が”Q1未満”という内容のものですね。

その通り。結果は「3」だね

確かに、この条件のチームは、1位のヴィッセル神戸、2位の横浜F・マリノス、9位のセレッソ大阪の3チームですからあってますね。

さすが、すぐに検証するというところはセンスがいいね。じゃあ、クロス集計表の「Q1未満」×「下位9チーム」に入れる式はどうなる

順位の条件を変えればよさそうですね「=COUNTIFS(順位,”>9″,四分位,”Q1未満”)」であってますか?

素晴らしい。正解です。この要領で他のセルも入れられるね。
(6)上位9チーム、下位9チームの積み上げ棒グラフ

最後に今のクロス集計表をグラフにしてみよう。グラフにすることでより視覚的に上位チームと下位チームの違いが比較できるよ。

はい。比較するってことは、上位チームのグラフと、下位チームのグラフを横に並べるとよさそうですね。

そうだね。今回は「積み上げ棒グラフ」を作って比較してみよう。

よろしくお願いします。

データを選択して、[挿入]→[グラフの挿入]→[縦棒]→[積み上げ縦棒]を選択してみて・

はい。グラフが表示されましたが、なんかちょっとイメージが違いますね。グラフの横軸を、上位9チーム、下位9チームしたいんですけれど。
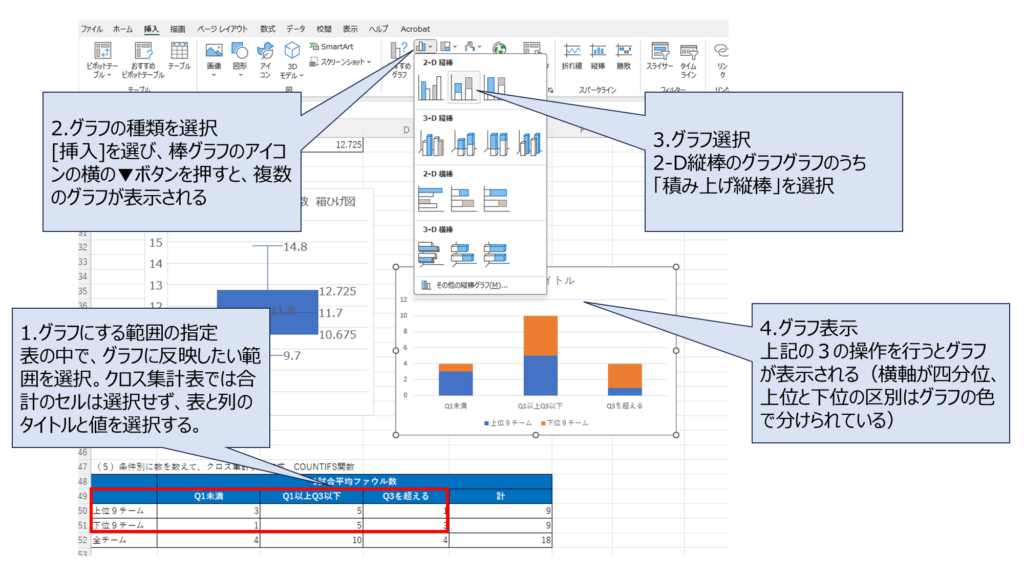

そうだね。エクセルは表の並びにしたがってグラフを自動的に作成するので、期待通りのグラフにならないことがあるんだ。

どうすればよいのですか?

今回は簡単だ。縦軸と横軸が反対なので、これを入れ替えればよいんだ。グラフを選択して右クリックし、[データソースの選択]を行い、「行/列の切り替え」をクリックしてみて。
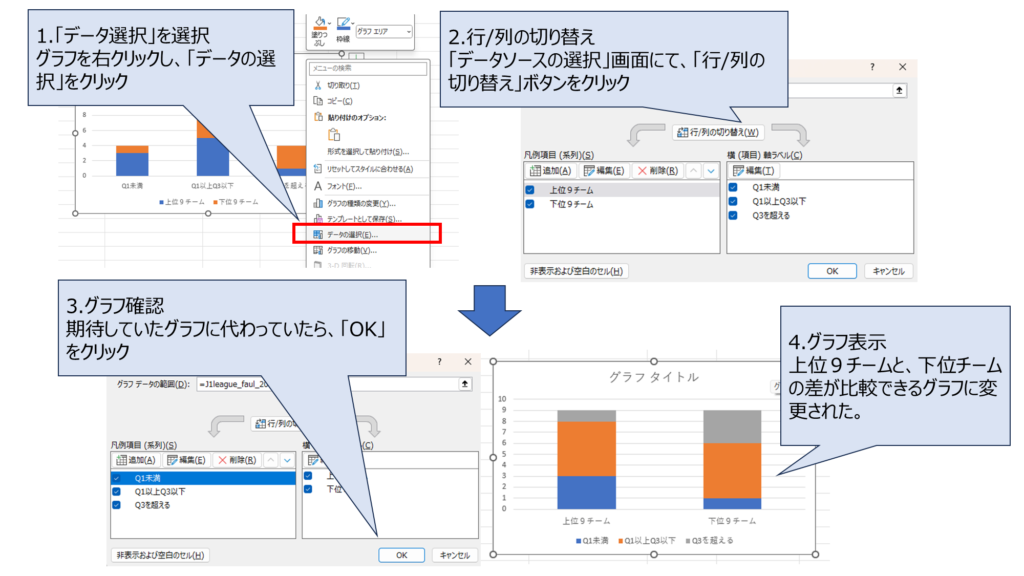

おお、期待通りのグラフになった!

さらに、タイトルやラベル、区分線をつけるとさらに分析しやすくなるよ。以下の手順で設定してみて。
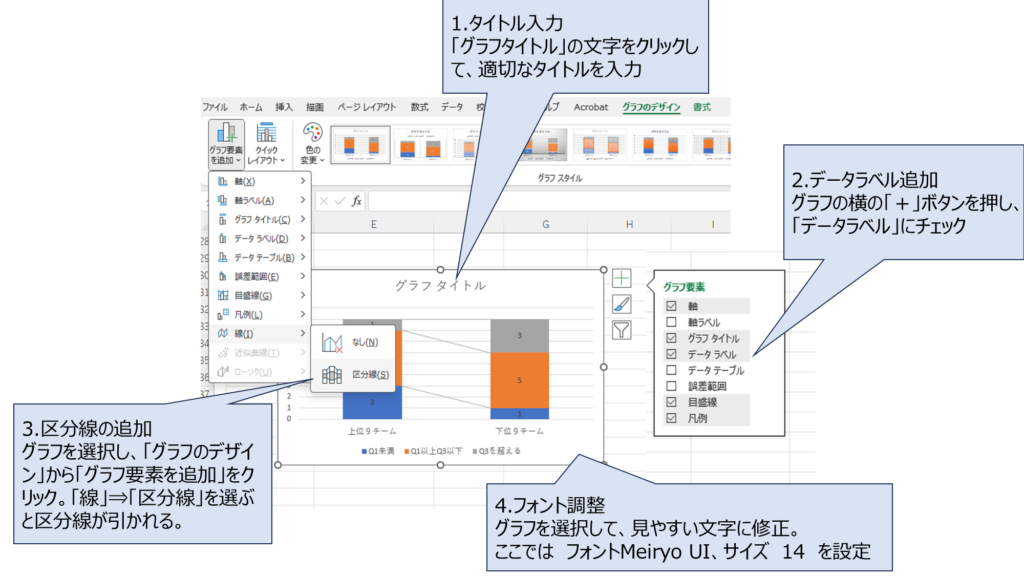

これで完成ですね。完成エクセルは J1league_faul_Cross_2023.xlsx です。グラフを見ると、データが視覚的にすごく分かりやすいですね
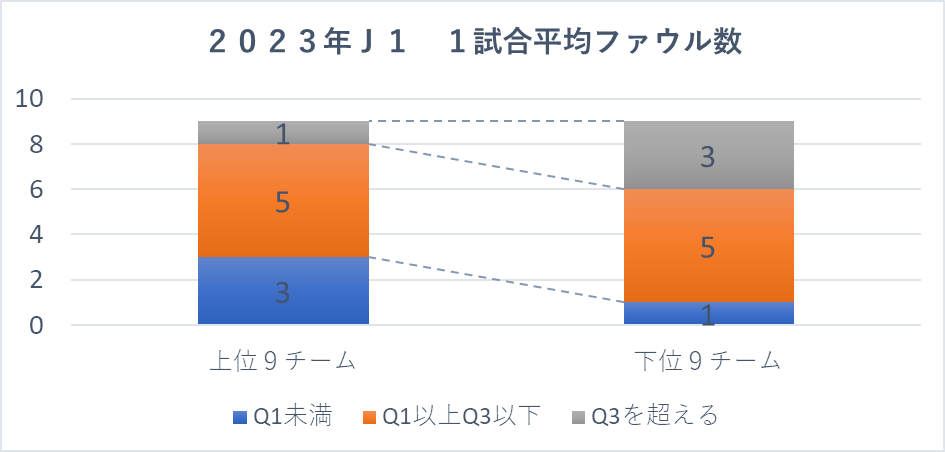

グラフからどんなことが分かるかな?

全体的に見ると、「Q1以上Q3以下」の範囲に分布するチームが10チームと多く、J1リーグ全体では平均的なファウル数の範囲に収まるチームが多いことが分かりますね

なるほど。では上位と下位との差はどこにあるかな?

上位チームは「Q1未満」のチームが多いことが特徴ですね。これは、ファウル数を抑えることが上位に入るための重要な要素になっているのかもしれません

その通りだね。逆に下位チームではどうかな?

下位チームでは「Q3を超える」チームが目立ちます。ファウルが多いと、カードを受けたり、相手にセットプレーのチャンスを与えたりして不利になりますから、それが順位に影響している可能性がありますね

素晴らしい考察だね。ファウルが少ないことで、試合のペースを自分たちでコントロールしやすくなるのもポイントだよ
今後の活用方法

クロス集計表による分析をおこなってみてどうだったかな?

データを収集する段階で、どの基準を軸にして比較したいかを考えることで、より有益な分析結果が得られそうですね。

そうだね。目的を明確にしてデータを収集すれば、無駄を減らして効果的な分析ができるようになるね。データ分析に関して、ずいぶん理解が深まったね。
まとめ
- クロス集計表
データを2つ以上の基準で分類し、各カテゴリのデータの分布や関係性を視覚化するための表である。 - 表頭/表側
クロス集計表におけるデータ分類の軸となる部分。行方向を「表側」、列方向を「表頭」と呼ぶ。 - マイクロソフト エクセル
データの整理・分析・視覚化を効率よく行うための表計算ソフトウェア。関数やグラフ作成機能が充実している。 - 四分位数
データを4つの部分に分ける指標であり、Q1(第一四分位数)、Q2(中央値)、Q3(第三四分位数)などを用いる。 - クロス集計表の作成方法
集計したい2つの項目を確認し、それぞれの分類を行と列に設定する。次に、対象データを手動で確認し、該当する行と列の交点に数を記入していく。
問題
「クイズをスタート」のボタンをクリックすると、5問出題します。さあチャレンジ!
編集者ひとこと
無事、「大学入学共通テスト情報Ⅰサンプル問題」の解説を完了しました。
2025年1月18日(土)・19日(日)の本番で、どんな問題が出題されるのか楽しみですね。この情報寺子屋を読んでしっかり学んでくれた人は、笑顔が待っていると思います。頑張っていこう!
<RANKING>![]()
高校教育ランキング



