2025年1月19日に行われました、情報Ⅰ共通テストの解説です。「+解答」と書かれた部分をクリックすると、解答と解説が表示されます。さあ!本番問題にチャレンジ!!
問題と解答はこちらから(PDF![]() )
)
第1問 小問集合
次の問い(問1 ~ 4)に答えよ。(配点20)
1-1 情報セキュリティ、通信プロトコル
a.次の文章中の空欄![]() に入れるのに最も適当なものを,後の(0)~(4)のうちから一つ選べ。
に入れるのに最も適当なものを,後の(0)~(4)のうちから一つ選べ。
インターネットで情報をやり取りする際 発信者が本人であることを確認するためにデジタル署名が利用できる。また,デジタル署名を用いると, その情報が![]() を確認できる。
を確認できる。
- 複製されていないか
- 暗号化されているか
- 改ざんされていないか
- どのような経路で届いたか
- 盗聴されていないか。
b.近年,128ビットで構成されるIPアドレスが利用されるようになった理由の一つとして最も適当なものを,次の(0)~(4)のうちから一つ選べ。![]()
- 有線LANだけでなく無線LANにも対応するため。
- 大容量データの送受信に対応するため。
- インターネットに直接接続する機器の増加に対応するため。
- 漢字など英数字以外の文字で表されるドメイン名に対応するため。
- HTMLの仕様変更に対応するため。
1-2 7セグメントLEDの表示方法
次の文章を読み,空欄 ![]() ~
~![]() に当てはまる数字をマークせよ。
に当てはまる数字をマークせよ。
図1に示した部品は,棒状の7個のLEDa~gを使って数字や一部のアルファベットを表示するものである。この部品を7セグメントLEDと呼び,例えば数字の0~ 9は図2のようにLEDを点灯させて表示することができる。
7セグメントLEDにおける,a~gを点灯させる組合せはすべてのLEDが消灯している状態を含めて全部で ![]()
![]()
![]() 通りである。
通りである。
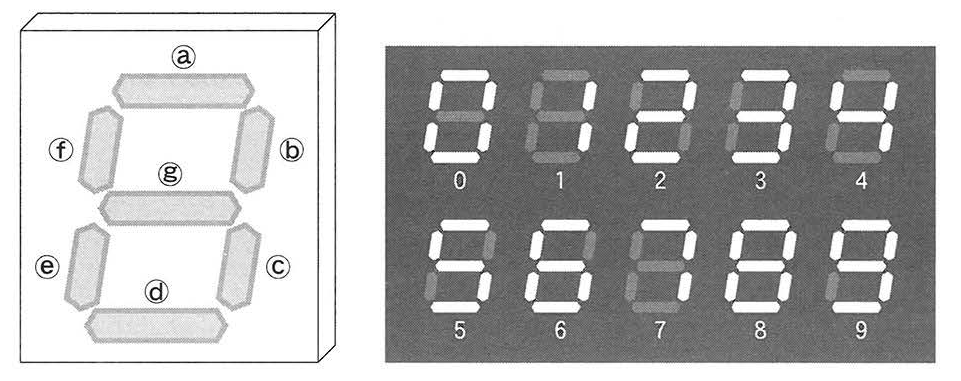
(右)図2 7セグメントLEDで表示した0~9の数字
正解
128
解説
7セグメントLEDは、各セグメントが点灯または消灯の2通りを持つため、総パターン数は 2^7 = 128 です。これには、すべて消灯する状態も含まれます。
図1に示した部品は,アルファベットとして図3に示す13種類を表示できる。
これらの大文字8種類,小文字5種類のアルファベットに加え,数字10種類を用いて,ある製品のエラーコードを表示する。図4のように, 1桁目を大文字のアルファベット, 2桁目を小文字のアルファベット, 3桁目以降の桁については数字のみを用いる場合図1の7セグメントLEDの部品が全部で少なくとも![]() 個あれば5,000種類のエラーコードを表示することができる。
個あれば5,000種類のエラーコードを表示することができる。
5000種類のエラーコードを表示するために必要な7セグメントLEDの部品数を求めよ。

正解
5
解説
1桁目:大文字アルファベット8種類
2桁目:小文字アルファベット5種類
3桁目以降:数字10種類
表示可能なエラーコードの総数は、部品数 N を用いると次の式で表されます:
8 * 5 * 10^(N-2) >= 5000
以上を解くとNの最小値は5
したがって必要なLED部品数は 5個 です。
1-3 チェックディジットの生成方法
次の文章を読み,空欄![]() に当てはまる数字をマークせよ。また,空欄
に当てはまる数字をマークせよ。また,空欄![]() に入れるのに最も適当なものを後の解答群のうちから一つ選べ。
に入れるのに最も適当なものを後の解答群のうちから一つ選べ。
チェックディジットは書籍のISBNコードなどで数字の入カミスを検出するためなどに利用されている。
ここでは 5桁の数字(N5N4N3N2N1)の利用者IDに,チェックディジット1桁(C)を加えた6桁の識別番号 (N5N4N3N2N1C)を考える。チェックディジットの生成方法として,次の 2種類を考える。
【生成方法A】 利用者IDの各桁の値を足し合わせ,10で割った余りRを求め,10からRを引いた値をチェックディジットとする。
【生成方法B】 利用者IDの各奇数桁(N5,N3,N1)の値をそれぞれ3倍にした値と,各偶数桁(N4,N2)の値を足し合わせ,10で割った余り Rを求め,10からRを引いた値をチェックディジットとする。
なおいずれの生成方法も,Rが0の場合はチェックディジットを0とする。
例えばある利用者IDが「22609」の場合にチェックディジットを計算すると,生成方法Aでは「1」になり,生成方法Bでは![]() となる。
となる。
正解
7
解説
奇数桁を3倍、偶数桁をそのまま足し合わせます。
奇数桁(2, 6, 9)
2×3 + 6×3 + 9×3 = 6 + 18 + 27 = 51
偶数桁(2, 0)
2+0=2
奇数桁、偶数桁合計
51 + 2 = 53
53 mod 10 = 3
チェックディジットは 10 - 3 = 7 となります。
これらのチェックディジットでは, 1桁の入カミスは検出できても2桁の入カミスは,検出できないことがある。生成方法Bはこの点について多少検出できるように工夫されている。
例えば![]() 入カミスをした場合は生成方法Aでは検出できることはないが, 生成方法Bでは検出できることがある。生成方法Aでは検出できないが、生成方法Bでは検出できる入力ミスは何か?
入カミスをした場合は生成方法Aでは検出できることはないが, 生成方法Bでは検出できることがある。生成方法Aでは検出できないが、生成方法Bでは検出できる入力ミスは何か?
- 奇数桁の数字を二つ間違える
- 連続する二つの桁の数字をそれぞれ間違える
- 奇数桁のうちの二つの桁の数字の順序を逆にする
- 連続する二つの桁の数字の順序を逆にする
正解
3:連続する二つの桁の数字の順序を逆にする
解説
生成方法Aは各桁の値を単純に足し合わせるため、連続する2桁の数字を入れ替えても合計値が変わらず、誤りを検出できません。
一方、生成方法Bでは奇数桁に重み(3倍)が付与されるため、連続する2桁の入れ替えによる誤差が反映され、誤りを検出することが可能です。
1-4 マウスカーソルの移動時間とユーザインタフェース
次の文章を読み,後の問い(a・b)に答えよ。
マウスカーソルをメニューやアイコンなどの対象物に移動する操作をモデル化し, Webサイトやアプリケーションのユーザインタフェースをデザインする際に利用されている法則がある。この法則では次のことが知られている。
- 対象物が大きいほど,対象物に移動するときの時間が短くなる。
- 対象物への距離が短いほど,対象物に移動するときの時間が短くなる。
a 次の文章中の空欄 ![]() に入れるのに最も適当なものを図5の0~3のうちから一つ選べ。
に入れるのに最も適当なものを図5の0~3のうちから一つ選べ。
この法則では, PCなどでマウスを操作する場合,マウスカーソルはディスプレイの端で止まるため,ディスプレイの端にある対象物は実質的に大きさが無限大になると考える。
この法則に基づくと,図5の0~3で示した対象物のうち,現在ディスプレイ上の黒矢印で示されているマウスカーソルの位置から,最も短い時間で指し示すことができるのは ![]() である。
である。
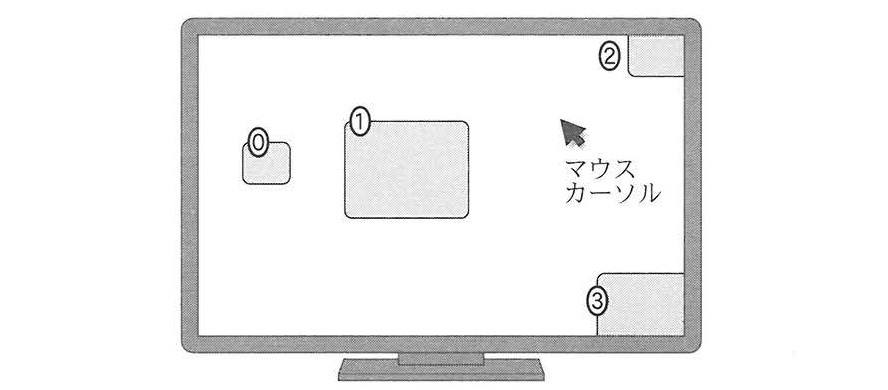
正解
2:C(ディスプレイ端のオブジェクト)
解説
ディスプレイ端のオブジェクトは「実質的に無限大の大きさ」とみなされるため、カーソルの移動時間が最短になります。
b 次の文章中の空欄![]() ・
・![]() に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
操作時間を短くするためにこの法則を適用した事例として,利用頻度に基づいてメニュー項目を配置する方法がある。
ここではマウスを右クリックした際に,マウスカーソルに対して図6に示すような位置で表示されるメニュー項目の配置について考える。マウスカーソルで選択できる各メニュー項目の大きさは同じであるとし, この法則のみに沿って設計されたとすると,「項目5」は他の項目と比べ利用頻度が![]() 項目なので,意図的に
項目なので,意図的に![]() に配置されていると考えられる。項目5の配置の理由は?
に配置されていると考えられる。項目5の配置の理由は?
- コの解答群
- 低い
- 同程度の
- 高い
- サの解答群
- メニューの中で一番目立つ場所
- マウスカーソルの位置から遠い場所
- マウスで素早く選択できる場所
正解
コ:0:低い
サ:マウスカーソルの位置から遠い場所
解説
項目5は、利用頻度が低い項目として意図的に配置されています。頻度が低い項目は、マウスカーソルから遠い位置や選択が容易でない場所に配置することで、重要度や利用頻度に応じた適切な設計が可能になります。この設計方針に基づいて、項目5が「利用頻度が低い」ことが理由となっています。
第2問-A 情報システムのデータの活用
A 商校生のYさんは,職業体験のため全国チェーンの総合スーパーマーケット「LikeWing」駒谷南店を訪れている。レジを担当したYさんと店長の会話文を読み,後の問い(問1~ 4)に答えよ。
Yさん:レシートにはたくさんの情報が印字されていますね(図1)。このレシートには「ポイント会員ID」が載っていますが,ポイントカードは店側にとってどんなよいことがあるのですか?
店長: LikeWing ではポイントカードを作成する際にお客様の名前, 性別生年の三つの属性情報をポイント会員情報として登録してもらっています。そして (A)ポイント会員情報とレシートに印字されている情報を組み合わせて分析することで販売促進につなげています。
Yさん:それらの情報には大切な情報も多いですよね。どう管理されているのですか?
店長:はい。ポイント会員情報とレシートに印字されている情報は,LikeWingの本部の情報システムで一括して管理しています。(B)本部,各店舗商品を製造するメーカー,商品を店舗に配送する配送センターの間で情報をやり取りしていて,商品は本部が一括して発注し,配送の指示を出します。
Yさん:LikeWingのネットショッピングサイトは有名ですね。そのネットショッピングサイトと,この情報システムはつながっているのですか?
店長: 今まさに連携を検討しているところです。これらが(C)連携するメリットは多くあります。
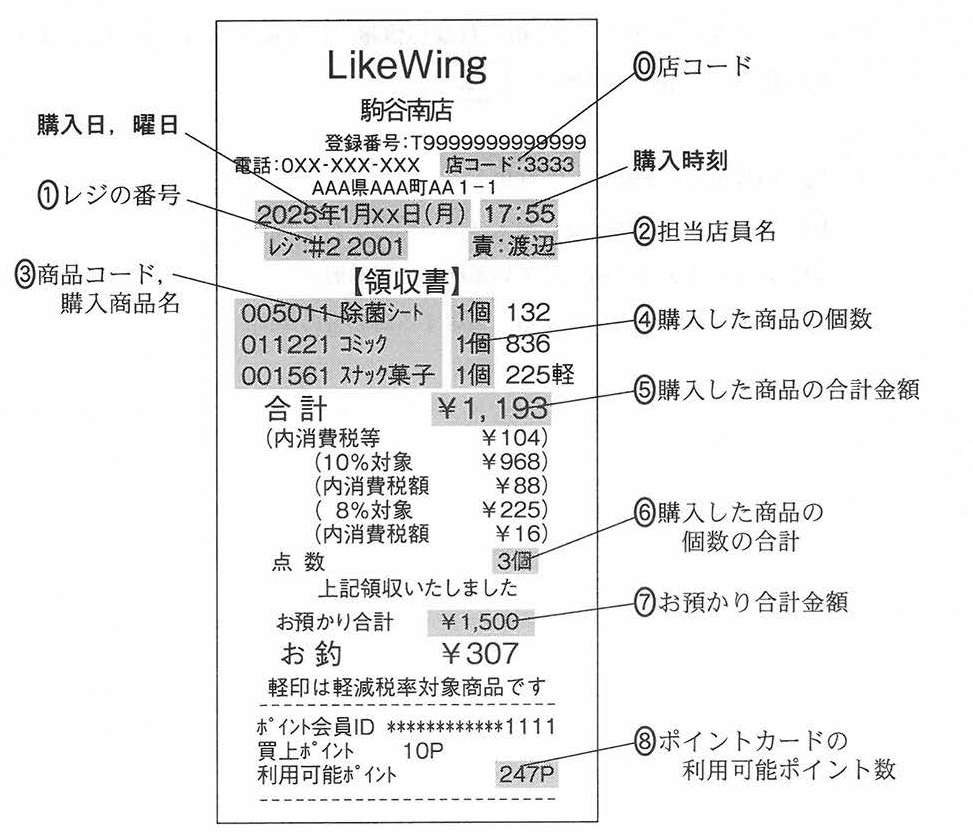
2A-1 データ分析に必要な情報
次の文章を読み,空欄![]() ~
~![]() に入れるのに最も適当なものを図1の0 ~8 のうちから一つずつ選べ。ただし, 空欄
に入れるのに最も適当なものを図1の0 ~8 のうちから一つずつ選べ。ただし, 空欄![]() ・
・![]() の解答の順序は問わない。
の解答の順序は問わない。
LikeWing全体での「時間帯ごとの総売上額(消費税込)」の比較を行うには,図1の「購入時刻」と「![]() 」に表されている情報から分析する。また, 「曜日別の各商品の購買の状況」を把握するには,図1の「購入日曜日」と「
」に表されている情報から分析する。また, 「曜日別の各商品の購買の状況」を把握するには,図1の「購入日曜日」と「![]() 」と「
」と「![]() 」に表されている情報から分析する。
」に表されている情報から分析する。
設問ア
正解
5:購入した商品の合計金額
解説
時間帯ごとの総売上額を比較するためには、購入時刻に加えて、購入した商品の合計金額が必要です。このデータを基に各時間帯の売上合計を算出できます。
設問イ、ウ
正解
3:商品コード、購入商品名、4:購入した商品の個数
解説
曜日別の購買状況を分析するためには、以下の情報が必要です:
2A-2 販売データの分析
下線部(A)の分析によって得られない情報として最も適当なものを次の0~3のうちから一つ選べ。![]()
- 顧客が商品を購入した理由。
- 同じ顧客に,繰り返し購入される傾向がある商品。
- ある商品を多く購入している顧客の年齢層。
- 年齢や性別の違いによる,来店する時間帯の傾向。
正解
0:顧客が商品を購入した理由
解説
購買データ分析では、購入商品の傾向や顧客属性の情報は得られますが、購入の理由については直接分析できません。この情報を得るには、アンケートなどの追加データが必要です。
2A-3 情報システム間の連携
図2は,下線部(B)に示すLikeWingの情報システムにおける主な情報の流れと商品の流れを表している。なお,顧客は必ずポイントカードを提示して商品を購入するものとする。
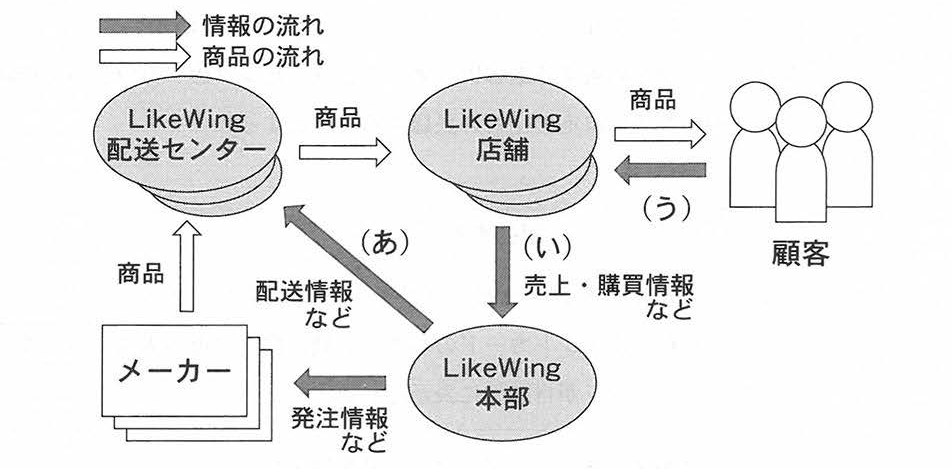
図2の中で,次のI、Ⅱの情報のそれぞれが必要とされる情報の流れ(図2のあ~う)を過不足なく含むものを,後の0~6のうちから一つずつ選べ。
- あ
- い
- う
- あ、い
- あ、う
- い、う
- あ、い、う
設問オ
正解
3:あ、い
解説
Iの情報「店コード」は、店舗から本部、配送センターへ送られる情報です。
設問カ
正解
5:い、う
解説
ポイント会員IDは、顧客の購買情報や会員情報を基にした分析に利用されます。この情報は、本部と店舗間で共有され、さらに商品配送や在庫管理にも関与します。したがって、ポイント会員IDは以下の流れに該当します。
い:ポイント会員IDを基に顧客情報を本部で管理する流れ。
う:顧客よりポイント会員IDを取得するための。
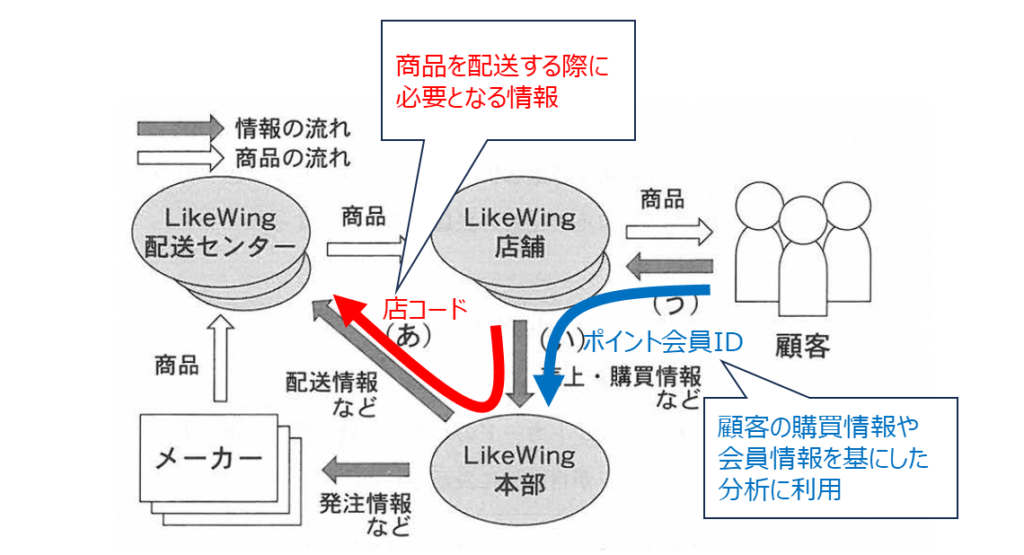
2A-4 情報システムに求められる条件
下線部(C)の連携するメリットとして,ⅢのI~Ⅲが考えられる。これらを実現するために後の【条件】あ~うのうち, LikeWingの情報システムに求められる条件はどれか。空欄![]() ~
~ ![]() のそれぞれについて,【条件】あ~うを過不足なく含むものを後の解答群のうちから一つずつ選べ。
のそれぞれについて,【条件】あ~うを過不足なく含むものを後の解答群のうちから一つずつ選べ。
なお, LikeWingのポイント会員であるか否かにかかわらず,ネットショッピングを利用する顧客は,ネットショッピングのアカウントを作成して,宅配のための自宅の住所を登録するものとする。

【条件】
- あ ポイント会員IDとネットショッピングのアカウントが対応付けられている。
- い ネットショッピングで扱われている商品に実店舗で用いられている商品コードが割り当てられている。
- う 商品コードと店コードから実店舗における商品の在庫数を調べることができる。
- あ
- い
- う
- あ、い
- あ、う
- い、う
- あ、い、う
設問 キ
正解
0:あ
解説
ポイントカードのポイント数や広告チラシを連携するためには、ポイント会員IDとネットショッピングアカウントの対応付け(あ)が必要です。
設問ク
正解
6:あ、い、う
解説
商品の在庫情報を表示するには、ポイント会員IDとネットショッピングアカウントの対応付け(あ)、実店舗の商品コードの連携(い)、店舗ごとの在庫数を把握する仕組み(う)が必要です。
設問ケ
正解
3:あ、い
解説
購買傾向を基におすすめ商品を提示するには、ポイント会員IDとアカウントの対応付け(あ)、商品コードの統一(い)が必要です。
第2問-B シミュレーション
次の文章を読み,後の問い(問1~3)に答えよ。
Mさんは,あるグループの会計係をしており10人のメンバーから一人6,000円ずつ集めることになった。Mさんは,以前集金をしたときにおつりに困ったことがあったので,メンバー全員におつりを渡すための千円札を何枚用意しておくのがよいか,次の条件でシミュレーションすることにした。
- グループのメンバーは来た順番に一人ずつMさんにお金を支払う。
- メンバーは,必ず千円札6枚(6,000円)または一万円札(10,000円)のいずれかでMさんに支払う。
- メンバーが一万円札で支払った場合,おつりの4,000円は千円札4枚で渡す。
- メンバーが千円札6枚で支払う確率を30%,―万円札で支払う確率を70%と考える。
シミュレーションは表計算ソフトウェアで1以上10以下の整数が同じ確率で出現する乱数rを用い,次のように考えて行った。
- が3以下の場合:千円札6枚で支払う
- rが4以上の場合:一万円札1枚で支払う
2B-1 モデルの作成とシミュレーション
次の文章を読み,空欄![]() ~
~![]() に当てはまる数字をマークせよ。
に当てはまる数字をマークせよ。
Mさんの手元の千円札の枚数を最初0枚として,シミュレーションをした結果表1のようになった。
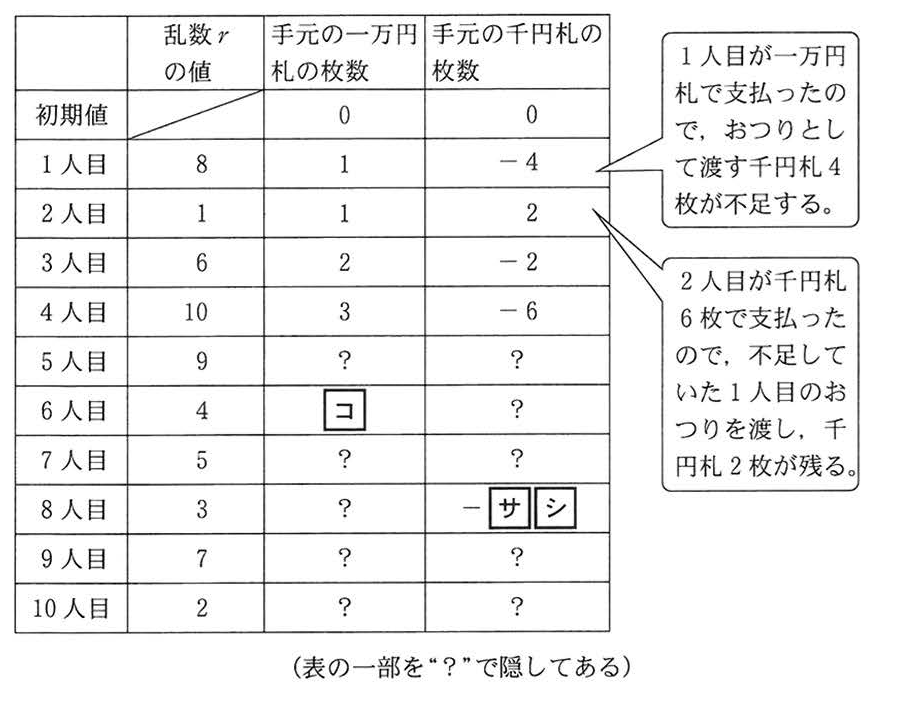
正解
コ:5、サシ 12
解説
乱数の値が3以下の場合、千円札+6
乱数の値が4以上の場合、1万円札+1、千円札ー6
増減する。表1に一万円札、千円札の増減数を示す列を追加し、表を完成させると以下の通り。
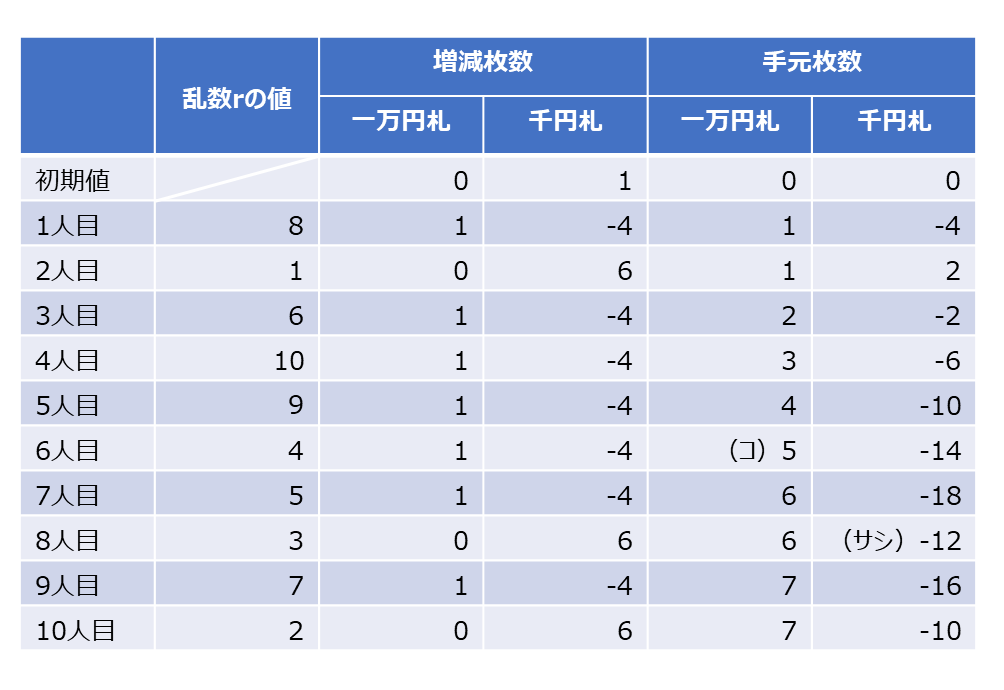
なお,この表の「手元の千円札の枚数」が負の数の場合,Mさんが渡さなければならないおつりの千円札が,その数の絶対値の枚数分不足していることを意味する。そこでMさんは「手元の千円札の枚数」の最小値を調べ,その絶対値の枚数の千円札を事前に準備しておけばおつりに困らないと考えた。
この考えによると,今回行った1回のシミュレーションの場合,千円札![]()
![]() 枚を事前に準備しておけば, 一度も千円札が不足することなく集金できることになる。
枚を事前に準備しておけば, 一度も千円札が不足することなく集金できることになる。
正解
18
解説
「手元の千円札の枚数」の最小値を求めます。表を見ると、7人目終了時点で「手元の千円札の枚数」が -18 になっています。この値が最小値です。したがって、事前に準備すべき千円札の枚数の絶対値は 18枚 です。
2B-2 シミュレーション結果の考察
M さんは, 1回のシミュレーション結果では判断できないと考え,このシミュレーションを10,000回行った。図3は各シミュレーションでの「手元の千円札の枚数」の最小値を横軸に,その回数を縦軸に表したものである。この結果に関する考察として最も適当なものを次の0~3のうちから一つ選べ。![]()
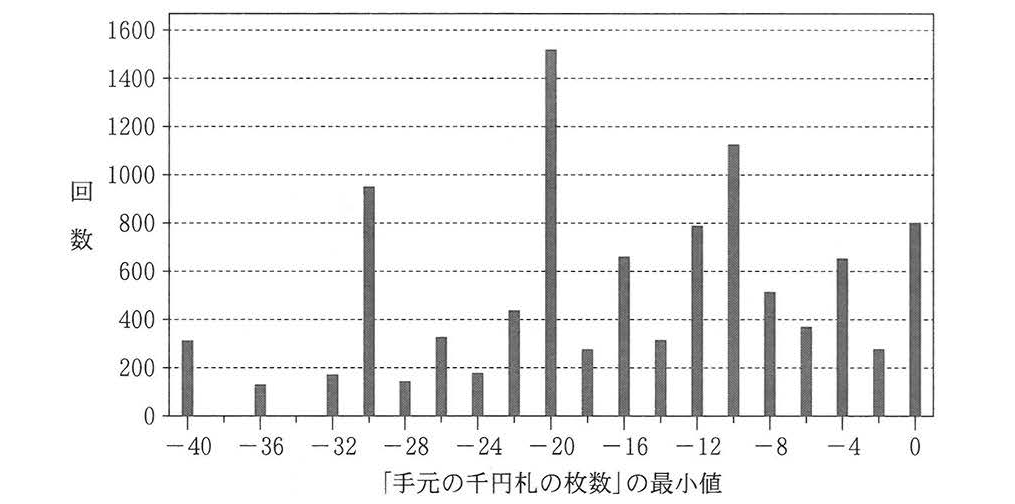
- 全員が一万円札で支払うケースはなかった。
- 最後まで千円札が不足しなかったのは,全回数の1割以下である。
- 別の乱数を使って10,000回シミュレーションを行っても最終的な結果のグラフはまったく同じになる。
- 全員が千円札でお金を支払ったケースが1回以上ある。
正解
1 選択肢 1「最後まで千円札が不足しなかったのは、全回数の1割以下である。」
解説
- 選択肢 0:誤り
全員が一万円札で支払うケースでは、最小値が -40 になると考えられます。図3を確認すると、最小値が -40 になる回数は 300回程度あり、選択肢0の主張は適切ではありません。 - 選択肢 1:正しい
図3を見ると、最小値が 0 になる回数は 800回程度 です。全体のシミュレーション回数は 10,000回 なので、割合は (800 / 10,000) = 0.08(8%) となり、「1割以下」という条件を満たします。よって、選択肢1は正しいと判断されます。 - 選択肢 2:誤り
別の乱数を用いた場合でも、シミュレーションの試行回数が多いと結果が統計的に収束するため、「グラフにばらつきが生じる」とする主張は適切ではありません。したがって、選択肢2は誤りです。 - 選択肢 3:誤り
全員が千円札でお金を支払った場合、最小値が 0 になることは可能性として含まれますが、全員が千円札で支払ったことを明確に示すわけではありません。また、図3の結果から「全員が千円札で支払ったケースが1回以上あるかどうか」を直接読み取ることは困難です。
2B-3 例外ケースの検証
次にMさんは事前に千円札を20枚用意した場合について考えた。この場合,メンバー10人から順に集金した際に起こることがないケースを0~3のうちから一つ選べ。![]()
- 最初の1人が千円札で支払ったとしても,途中でおつりの千円札が不足するケース。
- /用意された千円札をまったく使うことなく全員からの集金を終えるケース。
- 千円札で支払った人が5人いて,途中でおつりの千円札が不足するケース。
- 一万円札で支払った人が8人いて,途中でおつりの千円札が不足せず全員からの集金を終えるケース。
正解
選択肢 2「千円札でお金を支払った人が5人いた場合、一万円札で支払った人が5人いたことになる。」
解説
- 選択肢 0:誤り
最初の1人が千円札で支払い、残りの9人が一万円札で支払うケースでは、途中でおつりが不足するため、発生しえます。 - 選択肢 1:誤り
全員が千円札6枚で支払った場合、事前に千円札を使用することなく、集金を終えられます。 - 選択肢 2:正しい
千円札で支払った人が5人、一万円札で支払った人が5人のケースでは、事前に20枚の千円札を用意すれば不足が解消されるため適切です。 - 選択肢 3:誤り
最初の2人が千円札で支払い、3人目から10人目まで1万円でった場合は、以下の表のとおり、千円札が不足することはありません。

3問 アルゴリズムとプログラミング
第3問次の文章を読み,後の問い(問1~3)に答えよ。(配点25)
Kさんが所属する工芸部では毎年,文化祭に向けた集中製作合宿を開催し,複数の工芸品を部員全員で分担して製作している。Kさんは今年,工芸品を製作する担当の割当て作業を行うことになった。
3-1 ユースケースの理解
次の文章を読み,空欄![]() ~
~![]() に当てはまる数字をマークせよ。
に当てはまる数字をマークせよ。
表1は今年製作する各工芸品(1から順に番号を振る。)の製作日数である。製作日数は部員によって変わることはなく, 例えば工芸品1の製作日数はどの部員が製作しても4日である。なお,一つの工芸品の製作は一人の部員が担当し,完了するまでその部員は他の工芸品の製作には取り掛からない。

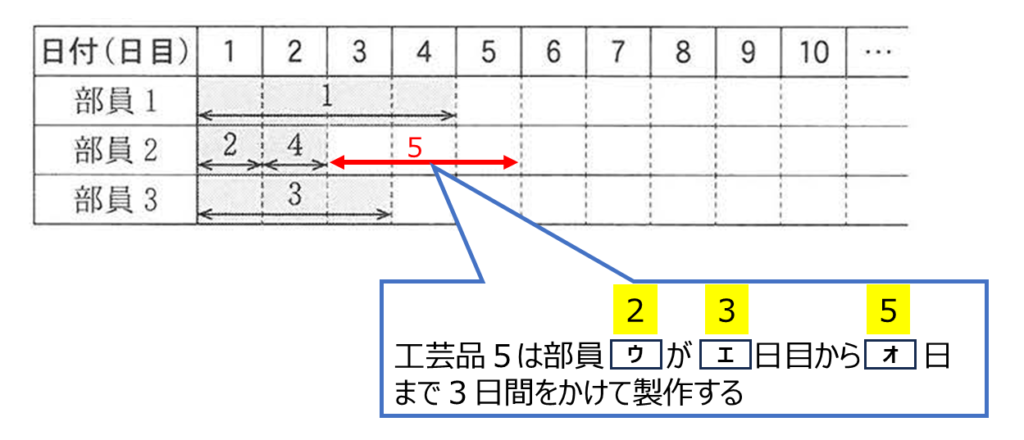
Kさんは図1の割当図を作成し,今年の工芸部の部員3名について,工芸品の番号順に割当てを決めていくことにした。
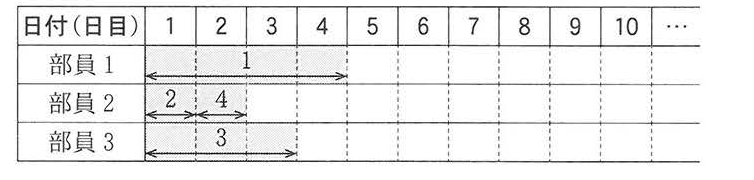
図1では最上段に日付を合宿初日から順に1日目,2日目, … と表して記載している。その下に各部員(1から順に番号を振る。)に割り当てた工芸品の番号を,その製作期間を表す矢印とともに記載している。例えば工芸品4は部員![]() が
が![]() 日目から1日間製作することが,図1から読み取れる。
日目から1日間製作することが,図1から読み取れる。
設問ア
正解
2
解説
図1を参照すると、工芸品4は部員2が担当しています。工芸品の割り当ては、空き日が最も早い部員に順に行われるため、部員2が割り当てられています。
設問イ
正解
2
解説
図1では、工芸品4の製作開始日は2日目と示されています。部員2は1日目に担当していた工芸品3の製作を終え、2日目から工芸品4の製作を開始しています。
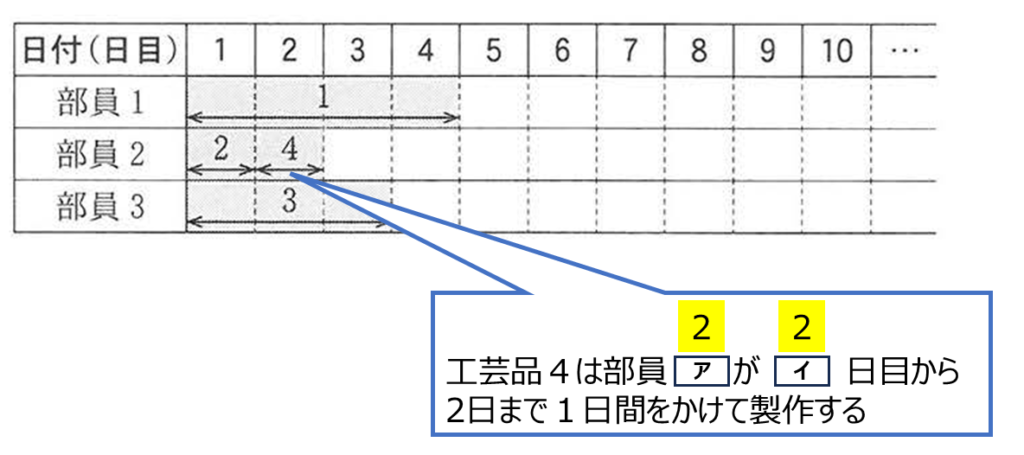
図1では工芸品4までが割り当てられており,部員1が5日目で割当てがない。このことを,部員1は5日目で空きであるという。
Kさんは各工芸品の担当と期間を割り当てていく際,次の規則を用いた。
| 最も早く空きになる部員(複数いる場合はそのうち最小の番号の部員)が,空きになった日付から次の工芸品を担当する。 |
Kさんは,工芸品5以降についても上の規則を用いて割り当て,各工芸品の担当と期間を一覧にした図2のような文面のメールを部員全員に送信した。
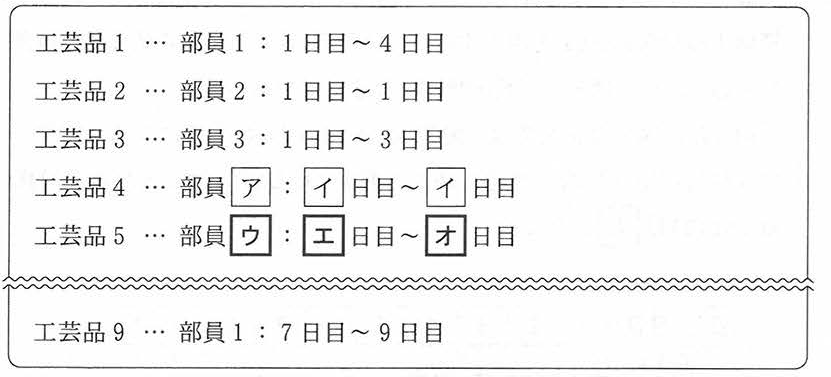
設問ウ
正解
2
解説
図1を参照すると、工芸品5は空き日が最も早い部員2が割り当てられます。
設問エ
正解
3
解説
図1では、工芸品5の製作開始日は3日目と読み取れます。
設問オ
正解
5
解説
図1では、工芸品5の製作日数が3日間と示されています。そのため、製作は3日目から開始され、4日目、5日目まで行われます。
以上を手作業で作成するのが手間だと感じたKさんは,図2のような文面を自動的に表示するプログラムを作成しようと考えた。
3-2 アルゴリズムの検討
次の文章を読み,空欄![]() 、
、![]() に当てはまる数字をマークせよ。また,空欄
に当てはまる数字をマークせよ。また,空欄![]() に入れるのに最も適当なものを後の解答群のうちから一つ選べ。
に入れるのに最も適当なものを後の解答群のうちから一つ選べ。
Kさんはまず,次の規則(再掲)に従い,いくつかの工芸品がすでに割り当てられた状況で,その次の工芸品の担当部員を表示するプログラムを作ることにした。
| 最も早く空きになる部員(複数いる場合はそのうち最小の番号の部員)が,空きになった日付から次の工芸品を担当する。 |
最も早く空きになる部員の番号を求めるために,各部員が空きになる日付を管理する配列Akibiを用意する。この配列の添字(1から始まる。)は部員の番号であり,要素はその部員が空きになる日付である。
例えば図1の状況では配列Akibiは図3のようになる。図1で部員1は5日目に空きになるため,図3で要素Akibi[1]は5となる。同様に要素Akibi[3]は![]() となる。
となる。

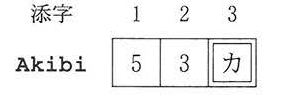
図3において,要素Akibi[ ![]() ]が配列Akibiの最小の要素であることから,部員
]が配列Akibiの最小の要素であることから,部員![]() が最も早く空きになることがわかる。
が最も早く空きになることがわかる。
正解
4
解説
部員3の空き日(Akibi[3])は、部員3が最後に担当する工芸品の製作終了日となります。図1の割り当て図によると、部員3は工芸品3を3日目まで担当するため、次に空きとなる日は4日目となります。
この考え方に基づき, Kさんは配列Akibiの要素と,部員数が代入された変数buinsuを用いて,次に割り当てる工芸品の担当部員を表示するプログラムを作成した(図4)。ここでは例として, (01)行目で図3のように配列Akibiを設定している。

- buin < tantou
- Akibi [buin] < Akibi [tantou]
- buin > tantou
- Akibi [buin] > Akibi [tantou]
正解
1 Akibi[buin] < Akibi[tantou]
解説
このプログラムは、「繰り返し処理」(ループ)を使用して、空き日が最も早い部員(tantou)を選択します。
条件としては、現在調査中の部員(buin)の空き日(Akibi[buin])が、現在の担当候補(tantou)の空き日(Akibi[tantou])よりも早い場合に、tantouを更新します。
具体的な流れ:

※:「特別講座」にPythonプログラムも掲載しているので、よかったらそちらの方も見てください。
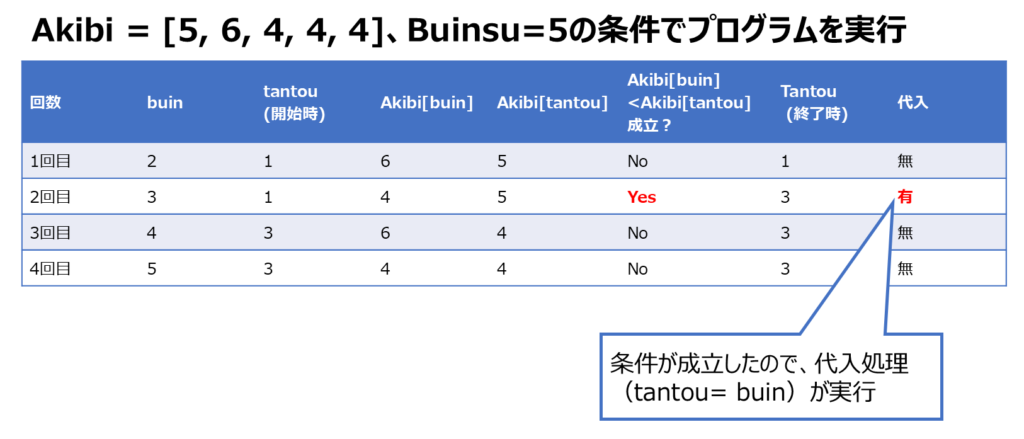
仮に部員数が変わったとしても配列Akibiと変数buinsuを適切に設定すればこのプログラムを用いることができる。部員が5名に増えた場 合 (01)行 目 を 例 え ば Akibi = [5, 6, 4, 4, 4]に (02)行目をbuinsu = 5に変更して図4のプログラムを実行すると,(06)行目の代入が![]() 回行われ,「次の工芸品の担当は部員3です。」と表示される。
回行われ,「次の工芸品の担当は部員3です。」と表示される。
正解
1
解説
プログラムの処理を順を追って確認すると、以下の通り。Akibi [buin] < Akibi [tantou]の条件が成立するのは、1回(2回目のループ処理の中)であることが確認できます。
3-3 プログラムの実装
次の文章を読み,空欄 ![]() ~
~![]() に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
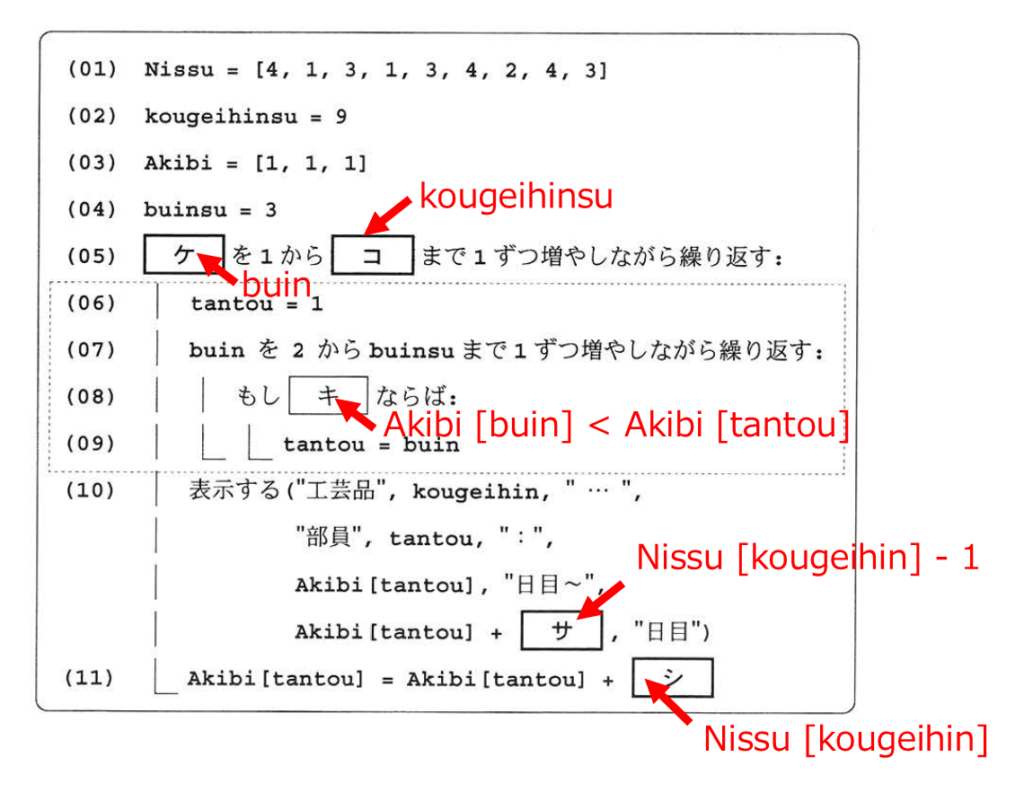
次にKさんは, 工芸部の部員数と,表1のような各工芸品の製作日数を用いて,図2のような一覧を表示するプログラムを作ることにした

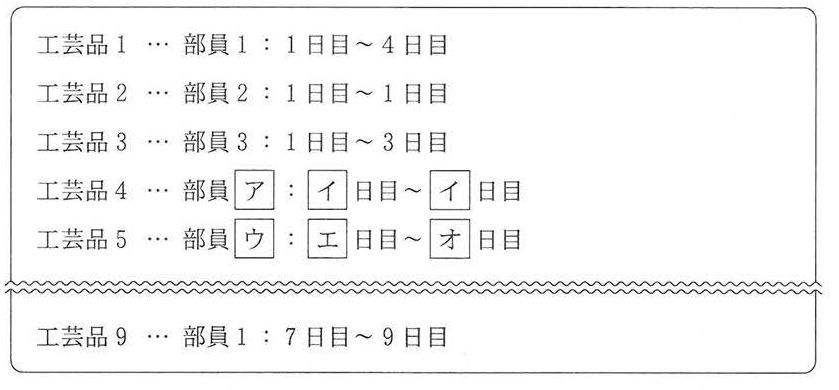
表1をプログラムで扱うために, Kさんは工芸品の番号順に製作日数を並べた配列Nissu(添字は1から始まる。)を用意した。さらに, 工芸品数9が代入された変数kougeihinsu, 各部員が空きになる日付を管理する配列Akibi, 部員数3が代入された変数buinsuを用いて,図2の一覧を表示するプログラムを作成した(図5)。
最初はどの部員も合宿初日すなわち1日目で空きであるため, (03)行目で配列Akibiの各要素を1に設定している。
工芸品の番号を表す変数kougeihinを用意し, (05)~(11)行目で各工芸品に対して順に担当と期間を求めていく。破線で囲まれた(06)~(09)行目は問2における図4の(03)~(06)行目と同じもので,次に割り当てる工芸品の担当部員の番号を変数tantouに代入する処理を行う。(10)行目で図2の1行分を表示し,(11)行目で担当部員が空きになる日付を更新する。

空欄 ![]() ~
~![]() に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
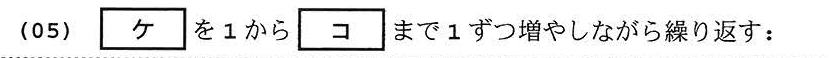
- buin
- kougeihin
- tantou
- buinsu
- kougeihinsu
設問ケ
正解
1 :kougeihin
解説
ケ は工芸品を1つずつ処理するためのループ変数として使われます。工芸品の番号を示す変数は kougeihin です。この変数を使って、製作日数や担当部員を判定します。
設問コ
正解
4 :kougeihinsu
解説
コ は工芸品の総数を表す変数です。工芸品の割り当てループはこの総数を基に実行されるため、終了条件として kougeihinsu を使用します。
空欄![]() ~
~![]() に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。

- Nissu [kougeihin]
- Nissu [tantou]
- Nissu [kougeihin] – 1
- Nissu [tantou] – 1
- Nissu [kougeihin – 1]
- Nissu [tantou – 1]
設問サ
正解
2: Nissu[kougeihin] – 1
解説
サ は工芸品の製作終了日を計算する部分です。開始日(Akibi[tantou])に製作日数から1を引いた値を加えることで、製作終了日を求めています。そのため、Nissu[kougeihin] - 1 が正しい式です。
設問シ
正解
0:Nissu[kougeihin]
解説
シ は担当部員の空き日を更新するために使用する値で、工芸品の製作日数そのものを加算します。そのため、Nissu[kougeihin] が正しい値です。
第4問 データの活用
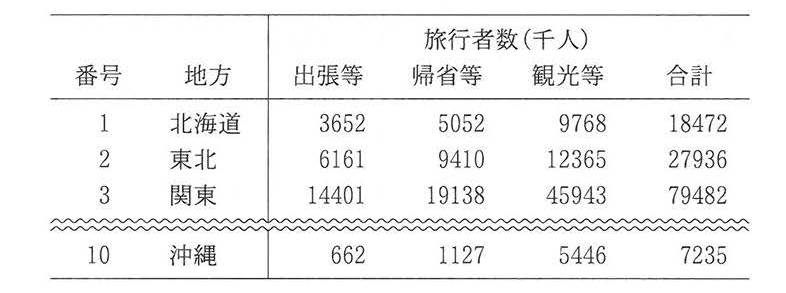
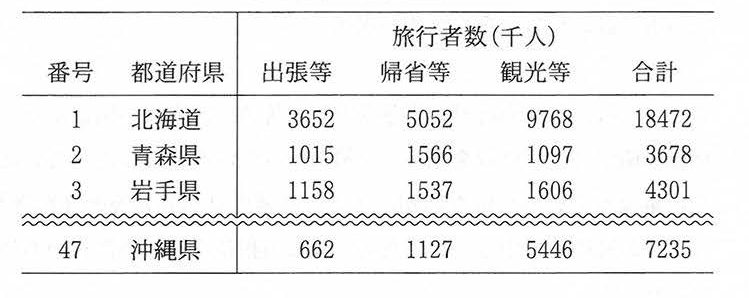
旅行が好きなUさんは観光庁が公開している旅行・観光消費動向調査のデータのうち, 2019年の結果を用いて,さまざまな観点で旅行に関する実態を分析してみることにした。なお,以下では延べ旅行者数を旅行者数と呼ぶ。
表1には地方ごとにその地方を主な目的地として宿泊旅行をした旅行者数がまとめられている。また,この表では,旅行の目的を出張等,帰省等,観光等の三つに分け,それぞれの旅行者数とその合計が集計されている。
4-1 尺度水準とグラムの読み取り
問1 次の文章を読み.空欄![]() ~
~![]() に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。ただし,空欄
に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。ただし,空欄 ![]() ・
・![]() の解答の順序は問わない。
の解答の順序は問わない。
Uさんは,表1を見せながら, T先生に相談した。
Uさん:この表からわかる情報を把握しやすくするために,グラフを作ろうと思っています。
T先生:グラフを作る前に表の各項目の尺度水準を確認してみましょう。地方については, どの尺度水準だと思いますか。
Uさん:郵便番号などと同じで![]() だと思います。
だと思います。
T先生:そうですね。では,番号と地方以外の項目については,どうでしょうか。
Uさん:これらの項目は旅行者数を示すので![]() でしょうか。
でしょうか。
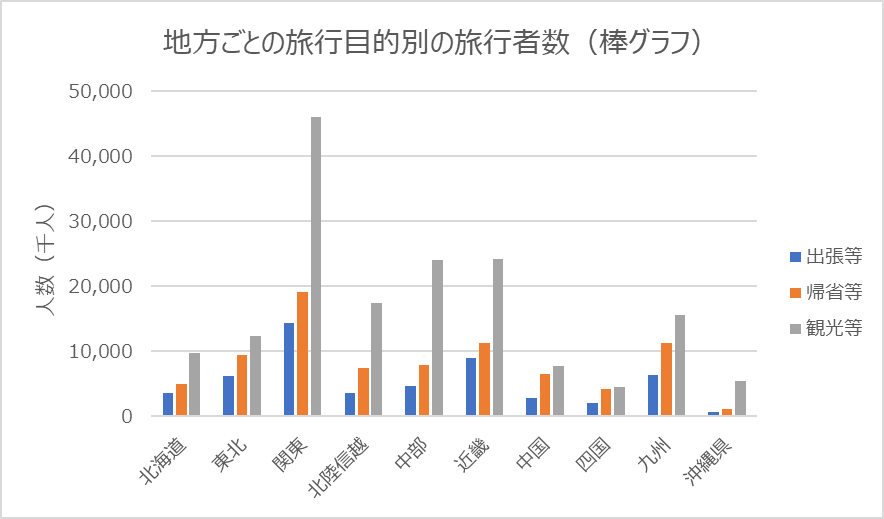
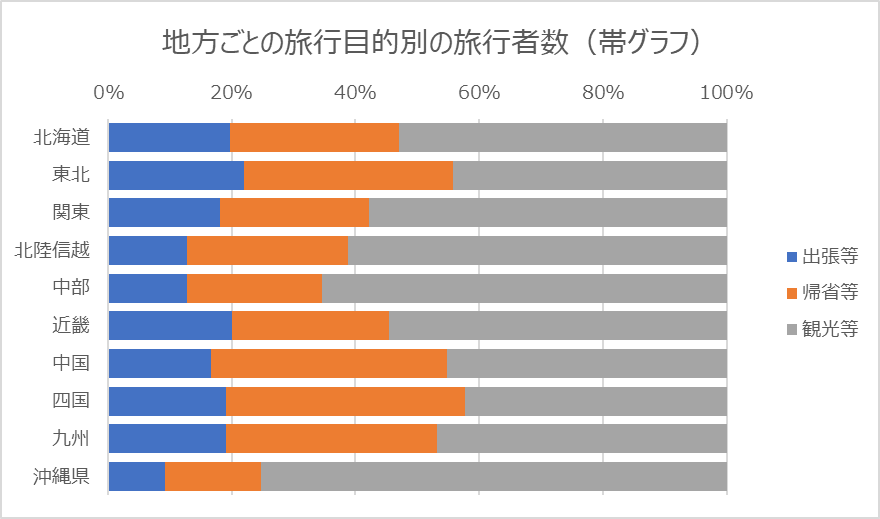
T先生:はい,そのとおりです。それでは地方による旅行者数の違いがわかりやすくなるように,棒グラフと帯グラフを作ってみましょう。
Uさんは,図1のグラフを作成した。これらのグラフから![]() ことや
ことや![]() ことなど,地方による傾向の違いを読み取ることができた。
ことなど,地方による傾向の違いを読み取ることができた。
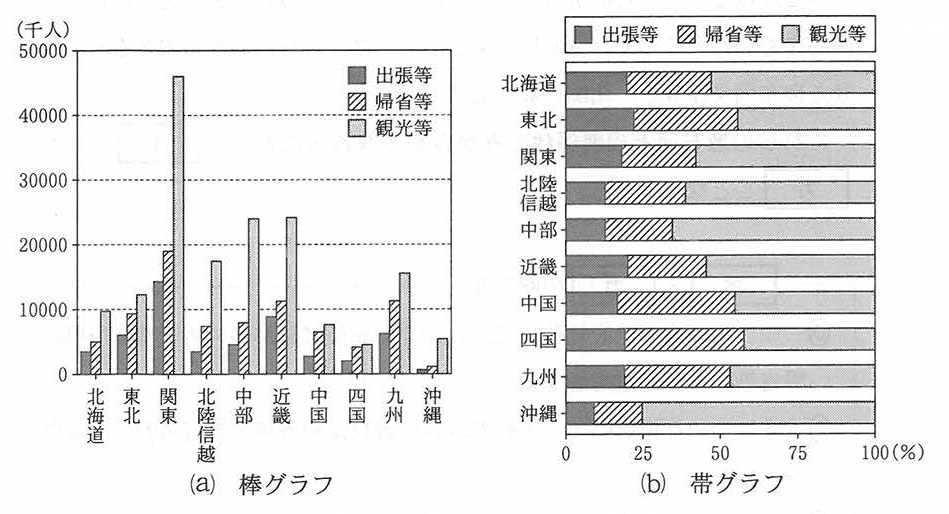
- 帰省等を目的とする旅行者数が最も多い地方は関東である
- 観光等を目的とする旅行者数が最も多い地方は沖縄である
- 地方ごとの旅行者数の合計に対する出張等の旅行者数の割合は,関東よりも東北の方が高い
- 地方ごとの旅行者数の合計に対する観光等の旅行者数の割合は,中部よりも近畿の方が高い
正解
0:帰省等を目的とする旅行者数が最も多い地方は関東である
2:地方ごとの旅行者数の合計に対する出張等の旅行者数の割合は、関東よりも東北の方が高い
解説
- 選択肢0:帰省等を目的とする旅行者数が最も多い地方は関東である
棒グラフ (a) を確認すると、関東地方の「帰省等(斜線部分)」の棒が他の地方と比較して明らかに最も高いことが確認できます。 - 選択肢1:観光等を目的とする旅行者数が最も多い地方は沖縄である
棒グラフ (a) では、観光等(グレーの部分)の旅行者数は、関東が最も多いため、本選択肢は正しくありません。 - 選択肢2:地方ごとの旅行者数の合計に対する出張等の旅行者数の割合は、関東よりも東北の方が高い
帯グラフ (b) を確認すると、東北地方の「出張等(黒い部分)」が旅行者数全体の割合で関東地方よりも明らかに高いことが確認できます。 - 選択肢3:地方ごとの旅行者数の合計に対する観光等の旅行者数の割合は、中部よりも近畿の方が高い
帯グラフ (b) にて、中部地方と近畿地方の「観光等(グレーの部分)」の割合を比較すると、中部の方が高いため、本選択肢は正しくありません。
4-2 散布図、相関係数
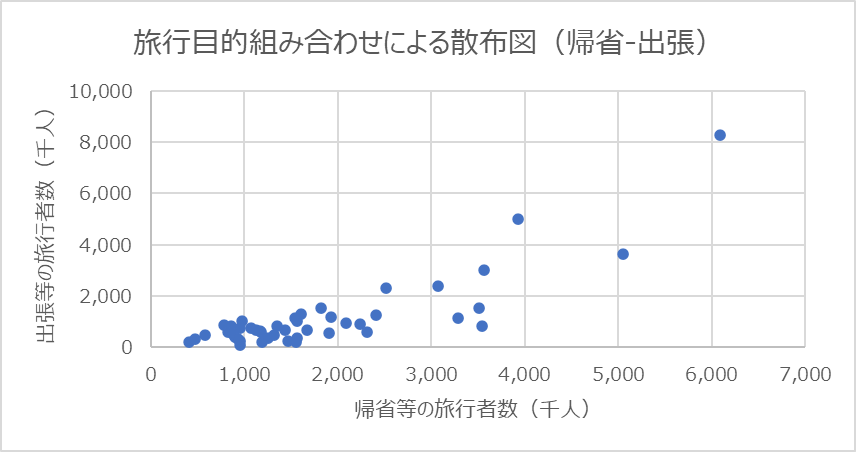
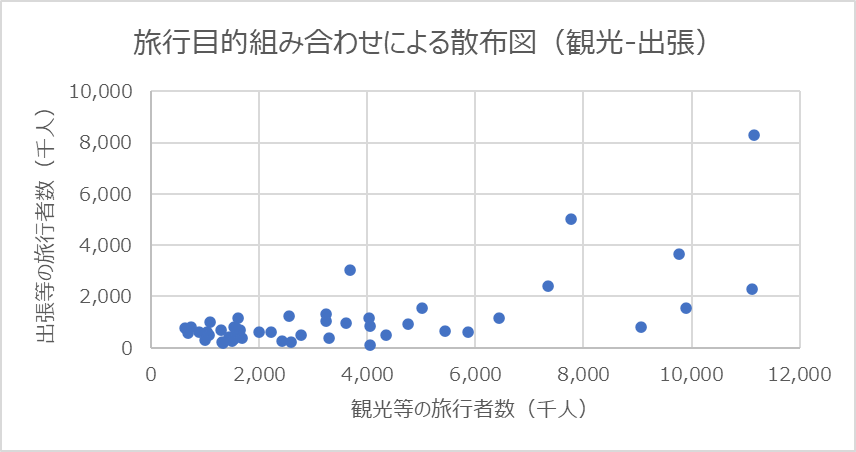
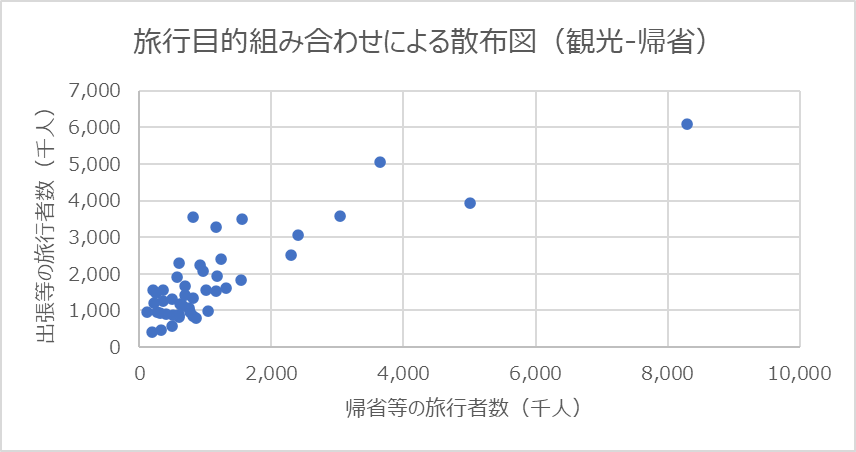
続いてUさんは,都道府県ごとの旅行者数と旅行目的別の内訳が集計されている表2をもとにさらに詳細な分析を進めることにした。
Uさんはここで,目的別の旅行者数の間にどのような関係があるかについて関心をもった。そこでUさんは,図2のように,各目的の旅行者数を組み合わせた散布図を作成し,相関係数を求めた。
これらの散布図と相関係数のみから読み取れることは![]() ことや,
ことや,![]() ことなどである。
ことなどである。
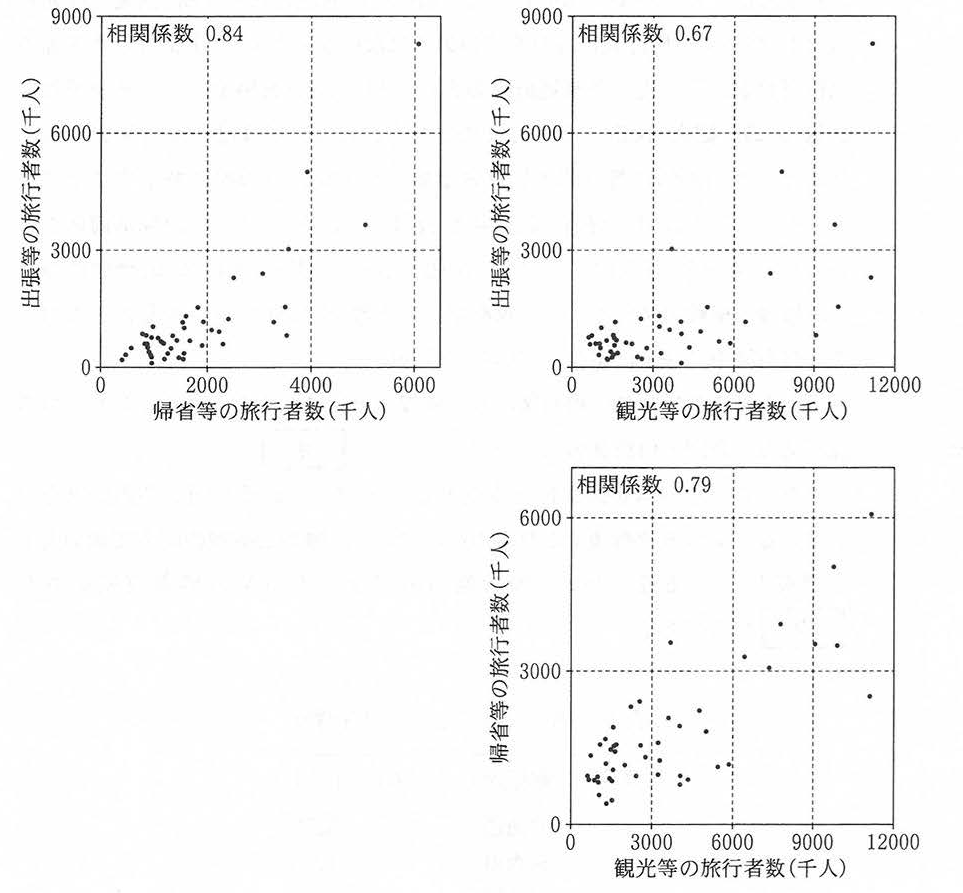
- 二つの都道府県を比較して,観光等の旅行者数が多い方の都道府県は帰省等の旅行者数も必ず多い
- すべての都道府県で出張等の旅行者数は帰省等の旅行者数の1.5倍を下回る
- それぞれの散布図で最も上に位置する都道府県は異なる
- 各都道府県について,ある目的の旅行者数が多くなるほど,他の目的の旅行者数も多くなる傾向にある
- 各都道府県で観光地をアピールすることで観光等の旅行者数を増やすことができれば,帰省等と出張等のいずれの旅行者数も増える
正解
1:すべての都道府県で出張等の旅行者数は帰省等の旅行者数の1.5倍を下回る
3:各都道府県について,ある目的の旅行者数が多くなるほど,他の目的の旅行者数も多くなる傾向にある
解説
- 選択肢0:二つの都道府県を比較して,観光等の旅行者数が多い方の都道府県は帰省等の旅行者数も必ず多い
観光等の旅行者数と規制等の旅行者数の関係を示す散布図(下図)を確認すると、正の相関が見られるものの、2つの都道府県を比較できる情報は記されていないため、「必ず多い」という条件を満たすわけではありません。 - 選択肢1:すべての都道府県で出張等の旅行者数は帰省等の旅行者数の1.5倍を下回る
図2の「出張等と帰省等の旅行者数」の散布図を見ると、すべてのデータ点が「帰省等の旅行者数 × 1.5」の直線以下に収まっていることが確認できます。これにより、出張等の旅行者数が帰省等の旅行者数の1.5倍を超える都道府県が存在しないことが読み取れます。
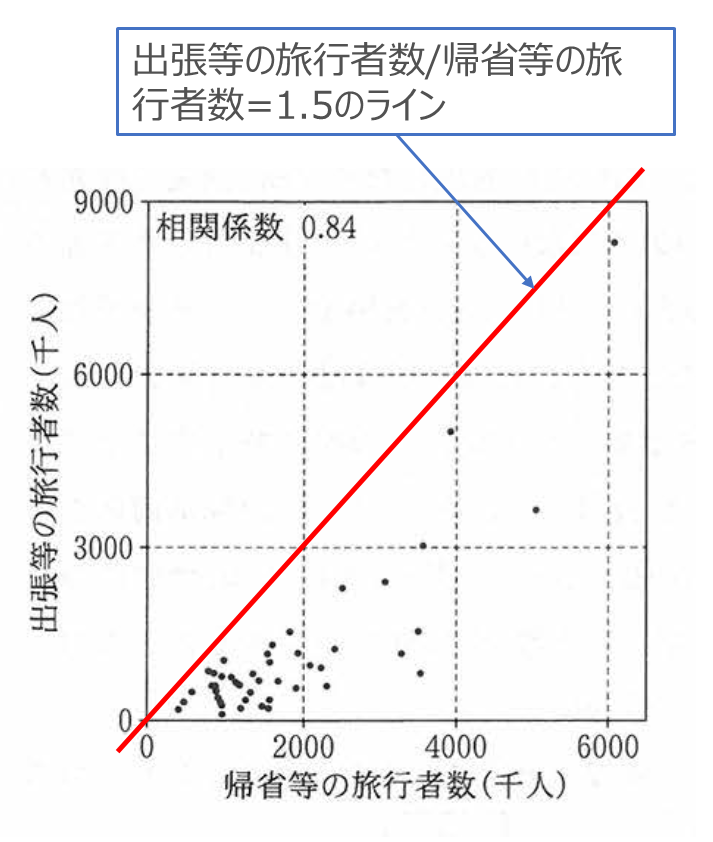
- 選択肢3:各都道府県について,ある目的の旅行者数が多くなるほど,他の目的の旅行者数も多くなる傾向にある
図2の散布図では、相関係数がそれぞれ 0.84、0.67、0.79 と正の値を示しており、各目的の旅行者数間で正の相関が存在することが確認できます。 - 選択肢4:各都道府県で観光地をアピールすることで観光等の旅行者数を増やすことができれば,帰省等と出張等のいずれの旅行者数も増える
図2の散布図は現在のデータに基づく相関関係を示しているのみであり、「観光地をアピールする」という仮定の下で帰省等や出張等の旅行者数が増えるという「因果関係:を示しているわけではありません。
4-3 新しい指標の設定と散布図の読み取り
問3 次の文章を読み,空欄![]() ・
・![]() に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
Uさんは各都道府県の出張等と観光等の旅行者数の関係に着目し,縦軸と横軸の値が等しい直線を記入した散布図(図3)を作成した。この散布図中に完全に重なっている点はないが多くの都道府県が観光等の旅行者数が3000千人以下の範囲に集中しているため,異なる指標を使った散布図も作成することにした。
Uさんは,人口が多い都道府県には旅行の目的地になる場所(企業や観光名所など)が多く,旅行先になりやすいのではないかと考え, 「出張等と観光等の旅行者数を,旅行先の各都道府県の人口で割った値」を指標とし,それぞれを出張/人口,観光/人口と呼ぶことにした。これらの指標は,旅行先の人口を基準として相対的に各目的の旅行者が多いか少ないかの程度を示すことになる。そこでUさんは,総務省統計局が公開している2019年度の都道府県ごとの人口のデータ(表3)を入手し,「出張/人口」と「観光/人口」の組合せについて,縦軸と横軸の値が等しい直線を記入した散布図(図4)を作成した。なお,この散布図中に完全に重なっている点はない。
図3と図4のいずれの散布図にも,直線の上側に白抜きの丸で示した二つの点がある。各図の白抜きの二つの点について![]() 。
。
また,これらの散布図上にある点Xと点Yは,それぞれ同じ都道府県を示している。二つの散布図でこれらの点について,縦軸と横軸の両方で値の大小が逆転している理由は, 点Xの都道府県よりも点Yの都道府県の方が![]() ためである。
ためである。
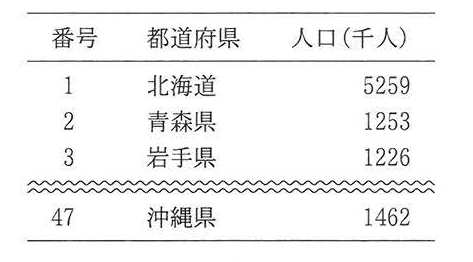
右:図4 「出張/人口」と「観光/人口」の組合せによる散布図
設問キ
- 両方の図で同じ二つの都道府県を示している
- 一つは両方の図で同じ都道府県を示し, もう一つは異なる都道府県を示している
- 両方の図で異なる二つの都道府県を示している
- これらの図からだけでは同じ都道府県であるかはわからない
設問ク
- 出張等の旅行者数が多い
- 観光等の旅行者数と出張等の旅行者数の差が大きい
- 観光等の旅行者数を出張等の旅行者数で割った値が小さい
- 人口が少ない
設問 キ
- 正解 0:両方の図で同じ二つの都道府県を示している
- 解説 同一都道府県における人口は不変であるため、 「旅行/人口 > 観光/人口」の条件を満たす点も、割合の散布図で同じ2点となります。
設問ク
- 正解 3:人口が少ない
- 解説
- 選択肢0: 出張等の旅行者数が多い
出張等の旅行者数が多いことは逆転の理由には直接つながりません。旅行者数の多さだけでは縦軸と横軸の大小関係を逆転させる理由として十分ではありません。 - 選択肢1: 観光等の旅行者数と出張等の旅行者数の差が大きい
観光等と出張等の旅行者数の差が大小逆転の原因になる場合もありますが、人口の影響を無視しては正確ではありません。この選択肢は部分的な説明に留まります。 - 選択肢2: 観光等の旅行者数を出張等の旅行者数で割った値が小さい
割った値が小さい場合、観光等と出張等の旅行者数の比率が変化することがありますが、それが縦軸と横軸の大小を逆転させる直接的な理由にはなりません。 - 選択肢3: 人口が少ない
人口が少ない都道府県では、「出張等/人口」や「観光等/人口」といった割合が人口の影響を受けやすくなります。これは相対的な値を大きく変化させ、散布図上での逆転現象を説明する最も合理的な理由です。
- 選択肢0: 出張等の旅行者数が多い
4-4 箱ひげ図、四分位数
問4 次の文章を読み,空欄 ![]() に当てはまる数字をマークせよ。また,空欄
に当てはまる数字をマークせよ。また,空欄![]() ~
~![]() に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
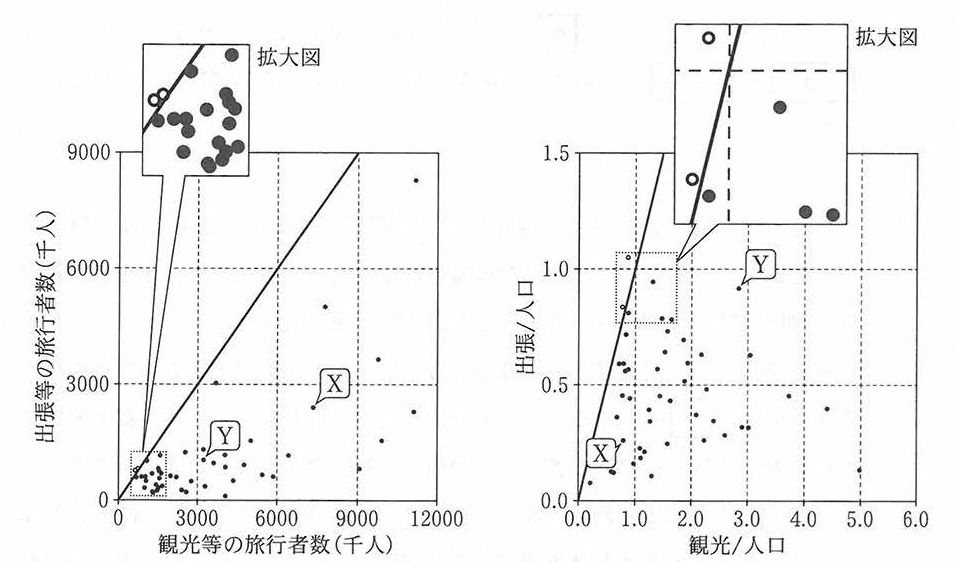
Uさんは,「出張/人口」と「観光/人口」の関係について,より詳しく分析することにした。そこで,図4の散布図の各軸に沿って各指標の分布を表す箱ひげ図(外れ値は0 で表記)を併記したもの(図5)を作成した。
図5を見ると,例えば観光等の旅行者が人口の4倍以上訪れる都道府県を表す点の数は ![]() 個である。このように,指標の値を見ることで,都道府県の人口に対して目的別の旅行者数がどの程度であったかを知ることができる。
個である。このように,指標の値を見ることで,都道府県の人口に対して目的別の旅行者数がどの程度であったかを知ることができる。
そこでUさんは,今回の分析において, 「出張/人口」がその第3四分位数より大きい都道府県を出張等が多めの都道府県, 「観光/人口」がその第3四分位数より大きい都道府県を観光等が多めの都道府県と呼ぶことにした。このように決めた場合![]() が最も多い。
が最も多い。
Uさんは, 「出張等も観光等も多めの都道府県」と, 「出張等は多めではないが観光等は多めの都道府県」がなぜそのような状況になっているのかに興味をもった。図5においてA~Fで示した都道府県のうち, 「出張等も観光等も多めの都道府県」は![]() である。一方「出張等は多めではないが観光等は多めの都道府県」は複数あるが,その中で「出張/人口」を「観光/人口」で割った値が最も小さい都道府県を考えると
である。一方「出張等は多めではないが観光等は多めの都道府県」は複数あるが,その中で「出張/人口」を「観光/人口」で割った値が最も小さい都道府県を考えると![]() となる。
となる。
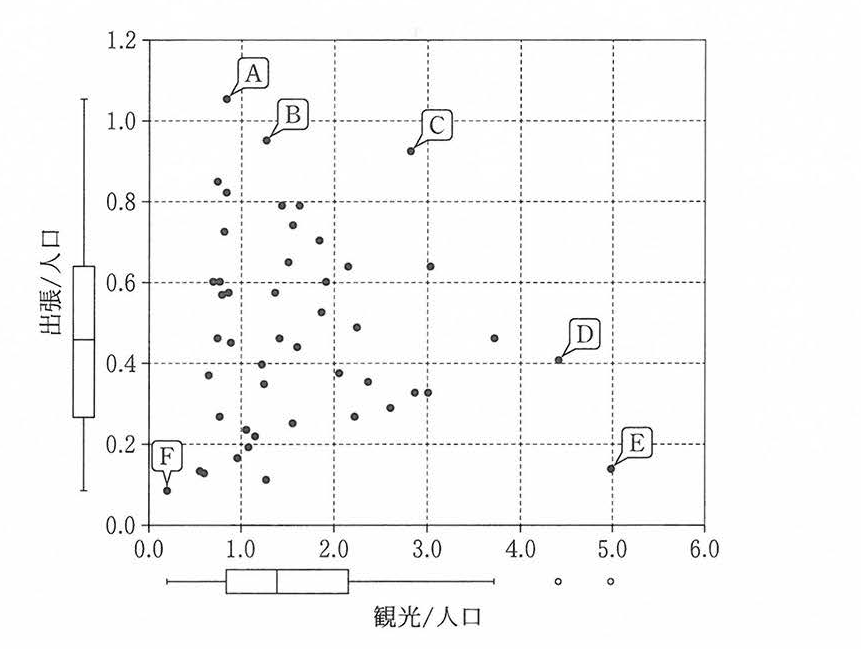
図5を見ると,例えば観光等の旅行者が人口の4倍以上訪れる都道府県を表す点の数は![]() 個である。
個である。
- 正解:2(D、E)
- 解説 図5の横軸「観光/人口」を見ると、観光等の旅行者数が人口の4倍以上訪れる都道府県を表す点は、D,Eの2つです。これにより、該当する都道府県数は2と判断されます。
今回の分析において, 「出張/人口」がその第3四分位数より大きい都道府県を出張等が多めの都道府県, 「観光/人口」がその第3四分位数より大きい都道府県を観光等が多めの都道府県と呼ぶことにした。このように決めた場合![]() が最も多い。
が最も多い。
- 出張等も観光等も多めの都道府県
- 出張等は多めではないが観光等は多めの都道府県
- 出張等は多めだが観光等は多めではない都道府県
- 出張等も観光等も多めではない都道府県
- 正解:3:出張等も観光等も多めではない都道府県
- 解説 図5を「出張等が第3四分位」「観光等が第3四分位」の境界に線を引き、4つに分割します。左下の領域に属する都道府県が最も多いことが図から読み取れます。この領域は、「出張等も観光等も多めではない都道府県」に該当します。
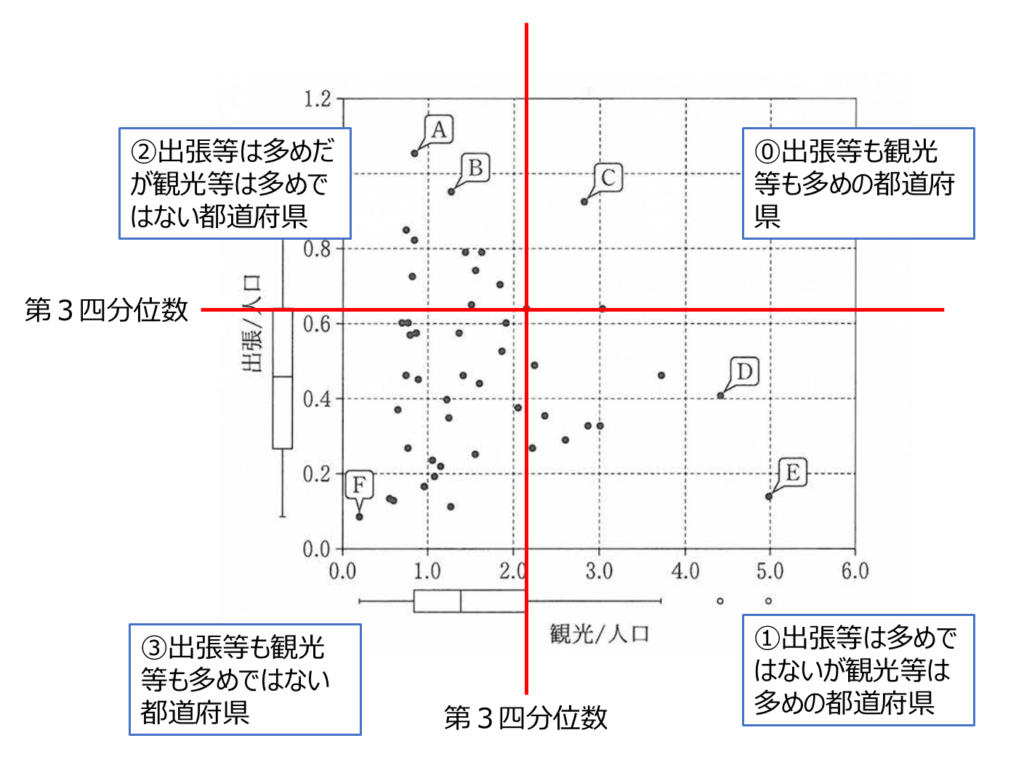
図5においてA~Fで示した都道府県のうち, 「出張等も観光等も多めの都道府県」は![]() である。一方「出張等は多めではないが観光等は多めの都道府県」は複数あるが,その中で「出張/人口」を「観光/人口」で割った値が最も小さい都道府県を考えると
である。一方「出張等は多めではないが観光等は多めの都道府県」は複数あるが,その中で「出張/人口」を「観光/人口」で割った値が最も小さい都道府県を考えると![]() となる。
となる。
- Aの都道府県
- Bの都道府県
- Cの都道府県
- Dの都道府県
- Eの都道府県
- Fの都道府県
設問サ
- 正解:2(C)
- 解説 図5を見ると、観光等(横軸)の値が大きく、出張等(縦軸)も高い値を示す点がCです。Cは観光等が特に多い都道府県として散布図上で確認できます。
設問シ
- 正解:4(E)
- 解説 図5においてA~Fに示した都道府県のうち「出張等は多めではないが観光等は多め」の都道府県は、DとEが該当する。グラフよりD,Eの値を比較すると以下の通り。分母がより小さく、分子がより大きいE の方が、割った値は小さくなることから、Eが該当します。
| 出張/人口 (1) | 観光/人口 (2) | (1)/(2) | |
| D | 大 | 小 | 大 |
| E | 小 | 大 | 小 |
特別講座(手を動かしてみよう)
第3問 Pythonプログラミング
第3問で出題された、「工芸品の担当部員割り当てプログラミング」をPythonでプログラミングして、実際に動かしてみましょう。
設問キ 次に割り当てる工芸品の担当部員を表示するプログラム
3-2の設問キで問われている、「図4 次に割り当てる工芸品の担当部員を表示するプログラム」をPythonでプログラミングしました。問題では配列Akibiの添え字は1から始まる条件となっていますが、Pythonの添え字は0始まりであるため、Akibi[0]にはダミーとして0を代入しています。
# 初期化(添え字0には、ダミー値0を代入)
Akibi = [0, 5, 3, 4]
buinsu = 3
tantou = 1
# 部員番号(インデックス2~buinsu)のループ処理
for buin in range(2, buinsu+1):
# 条件が成立すれば担当者 (tantou) を更新
if Akibi[buin] < Akibi[tantou]:
tantou = buin
# 最終結果の表示(部員番号は1から始まるように出力)
print(f"次の工芸品の担当は部員 {tantou} です")
本プログラムは、Google Colaboratory(略称: Google Colab)で実行可能です。Google アカウントさえあれば、次のリンクにアクセスして、実際に動作を確認することができます(リンク)
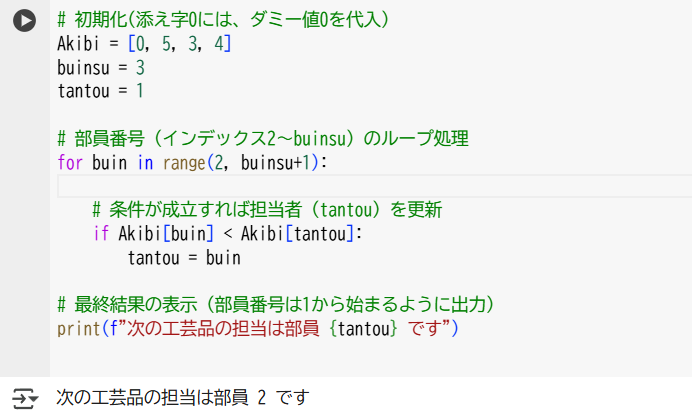
設問ク 処理トレース(ログ追加)
設問クでは、図4のプログラムが実行する際に、変数tantouに何回代入処理が行われるかを答える問題です。試験では、頭の中でプログラミングをトレースしましたが、ここではプログラムの中にログをついかして、実行中の変数の変化を可視化してみます。
# 初期化(添え字0には、ダミー値0を代入)
Akibi = [0, 5, 6, 4, 6, 4]
buinsu = 5
tantou = 1
# 部員番号(インデックス2~buinsu)のループ処理
for buin in range(2, buinsu+1):
# ループ開始時の状態を表示(部員番号は1から始まるように出力)
print(f"ループ開始: buin = {buin}, tantou(開始) = {tantou}, "
f"Akibi[buin] = {Akibi[buin]}, Akibi[tantou] = {Akibi[tantou]}")
# 条件が成立すれば担当者 (tantou) を更新
if Akibi[buin] < Akibi[tantou]:
tantou = buin
print(f" → 条件成立: tantou を {tantou} に更新")
else:
print(" → 条件不成立: tantou の更新はなし")
# 最終結果の表示(部員番号は1から始まるように出力)
print(f"次の工芸品の担当は部員 {tantou} です")google colabでの実行例は以下の通りです。(リンク)

実行した結果、ループの2回目で「条件成立」となり、変数tantouに代入処理が行われていることが分かりました。
・設問ケ~シ 各工芸品の担当と期間の一覧を表示するプログラム
設問ケ~シは、各工芸品の担当と期間の一覧を表示するプログラムの穴埋めになります。サ、シの設問では、変数Nissuに+1してみたり、してみなかったりでちょっと戸惑ったかもしれません。実際のプログラムを変更して、+1したら(しなかったら)どうなる?なども試してみると、より理解が深まると思います。
# 初期化(添え字0には、ダミー値0を代入)
Nissu = [0, 4, 1, 3, 1, 3, 4, 2, 4, 3]
kougeihinsu = 9
Akibi = [0, 1, 1, 1]
buinsu = 3
# 工芸品番号を1からkougeihinsuまで順に処理
for kougeihin in range(1, kougeihinsu + 1):
tantou = 1
# 部員番号を2からbuinsuまで確認し、Akibiの値が最も小さい部員を担当に選ぶ
for buin in range(2, buinsu + 1):
if Akibi[buin] < Akibi[tantou]:
tantou = buin
# 担当者が決まった後に工芸品の作業開始日と終了日を表示
print("工芸品", kougeihin, "…",
"部員", tantou, ":",
Akibi[tantou], "日目〜",
Akibi[tantou] + Nissu[kougeihin] - 1, "日目")
# 担当部員のAkibiを更新
Akibi[tantou] += Nissu[kougeihin]
google colabでの実行例は以下の通りです。(リンク)

第4問 エクセルを用いたデータ分析
4-1 地方別棒グラフ、帯グラフ
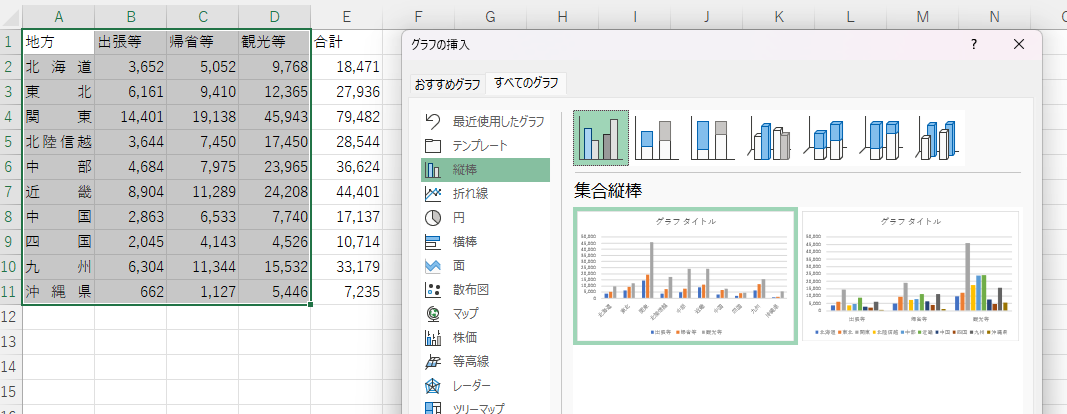
統計局「旅行・観光消費動向調査(2019年度版)」のデータより、エクセルにて描画しました。
完成したグラフのエクセルデータはこちらです(リンク(one drive)、リンク(ダウンロード))
実際に試験問題と同じグラフを作成してみると、棒グラフと帯グラフの目的の違いや、タイトルや軸の設定の仕方等、勉強になる点が多いので、ぜひ添付エクセルのデータをつかって、自分でも作成してみてください。
以下に簡単ですが、目的のグラフの作成方法を記します。
- 棒グラフ
- データ領域選択
- 「挿入」ー「グラフ」よりグラフの挿入ダイアログを表示
- すべてのグラフタブより、「縦棒」-「集合縦棒」を選択
- タイトル、軸ラベルの入力
- 帯グラフ
- データ領域選択
- 「挿入」ー「グラフ」よりグラフの挿入ダイアログを表示
- すべてのグラフタブより、「横棒」ー「100%積み上げ横棒」を選択
- タイトル、軸ラベルの入力
4-2 散布図と相関係数
次の散布図です。エクセルでは、グラフの中に相関係数を表示していませんが、CORREL関数を利用すると簡単に求めることが可能です。エクセルシートを見て、計算方法を確認してください。
また、エクセルでは近似曲線や回帰式を求めることもできるので、トライしてみてください。
以下に簡単ですが、目的のグラフの作成方法を記します。
- 棒グラフ
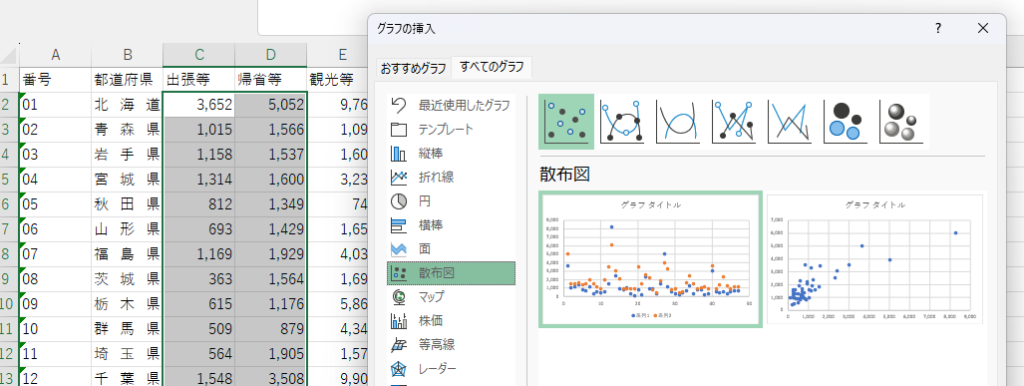
- 作成された散布図にて、X軸、Y軸の指定が必要な場合
- グラフを選択し、「グラフのデザイン」ー「データの選択」をクリックし、データソースの選択ダイアログを表示。
- 凡例項目(系列)の「編集ボタン」をクリックし、「系列Xの値」と「系列Yの値の内容」に軸として設定したいデータの列を指定
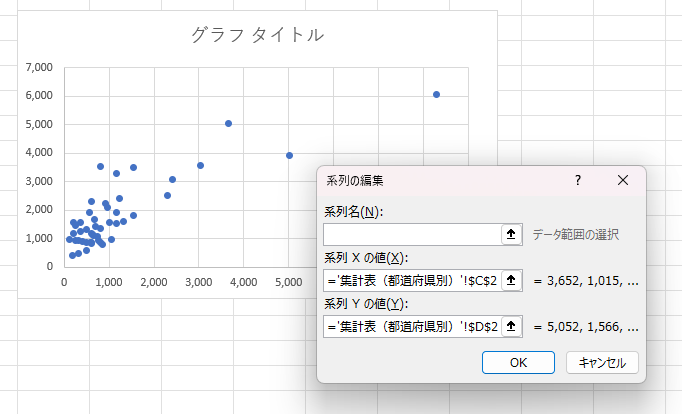
4-3 新たな指標を用いた散布図による分析
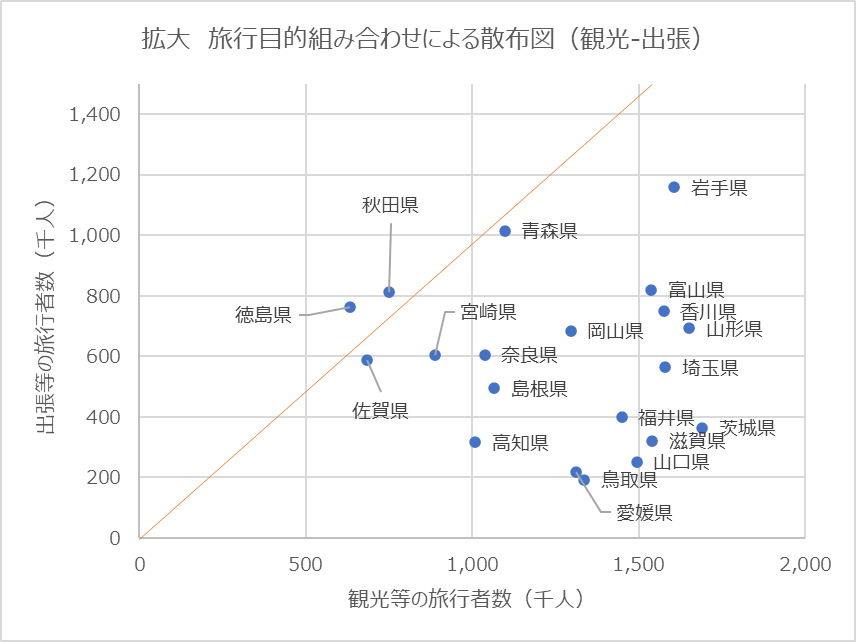
エクセルでは、データのプロットされた点に「ラベル」をつけることができます。今回は、問題で問われた直線の上側にある2つの点が目立つように軸のレンジを狭めてみました。実際にラベルを書いてみると、直線の上にある点は「秋田県」と「徳島県」であることが分かります。直線の上ということは、観光等の旅行者より出張等の旅行者の方が多いことを意味します。
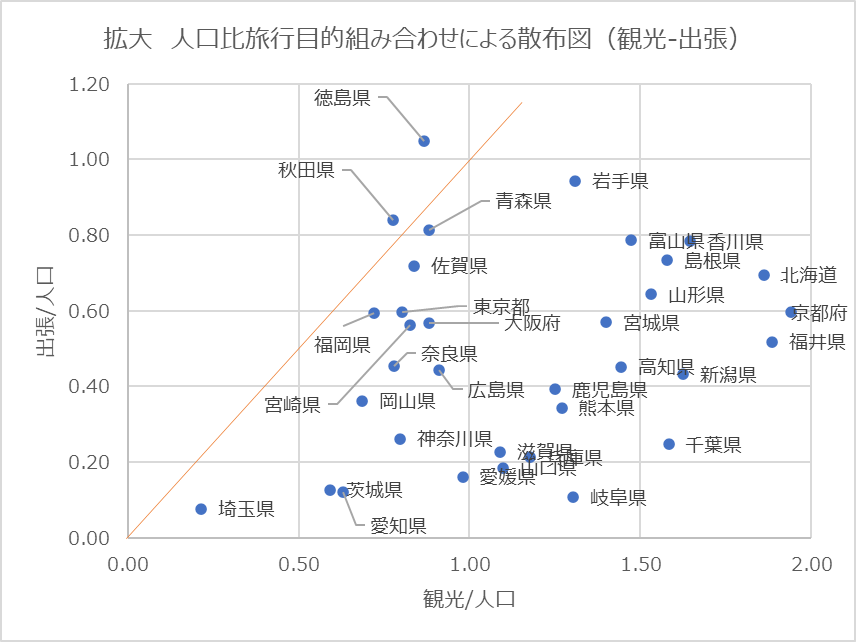
下のグラフは、縦軸、横軸を「人口」で割った際の散布図です。こちらも直線の上にある点は「秋田県」と「徳島県」です。しかし位置関係が逆になっていますね。
設問キを、実際のデータで考えてみましょう
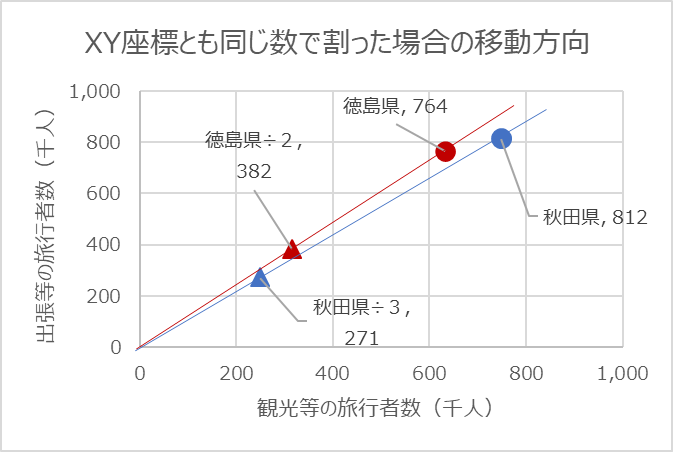
設問キの正解は「0:両方の図で同じ二つの都道府県を示している」でした。しかし、なぜそうなのか今一つ理解できない方もいるかもしれません。そこで実際のデータで見てみます。
図3の直線より上に来ている県は、「徳島県」と「秋田県」の2つ。これは観光などの旅行者数より、出張などの旅行者数の方が多い県になります。
図4ではX軸、Y軸をそれぞれの県の人口で割っています。仮に秋田県の人口が3千人、徳島県の人口を2千人とすると(そんなに少ないはずはないですが)、プロットされる点は上の図の▲マークの位置になります。これは、図の直線で示したx=0,y=0から引かれた直線上に位置しています。つまり、人口の大小によって図3と図4でそれぞれの県のプロットされる点の座標0からの位置関係は変わりますが、0からの角度は常に変わりません。
このため、設問キで問われている直線の上に位置する県は同じ都道府県になります。
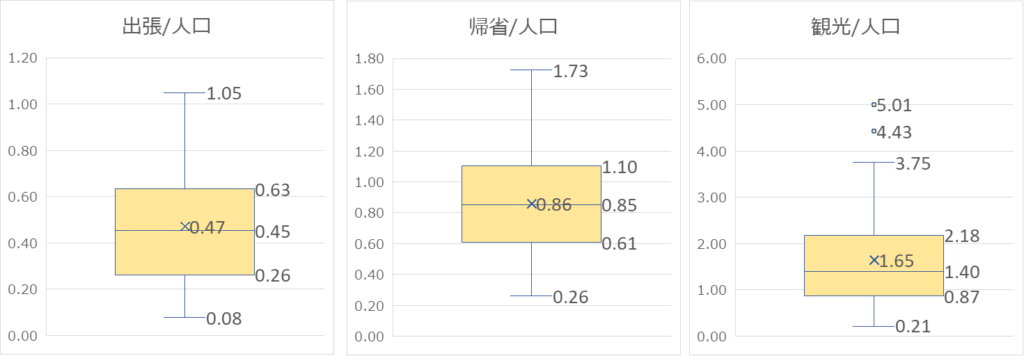
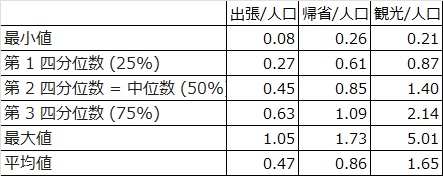
4-4 箱ひげ図による分析
せて、次は箱ひげ図です。問題の「図5」のように散布図と箱ひげ図を組み合わせて表示する機能はエクセルにはないので、ここでは箱ひげ図の見方のみを示します。
箱の中心にひかれた線は中央値(50%目のデータ)です。そして箱の上底:25%目、箱の上端が755%目、さらに箱の外のひげの部分が、最小値、最大値です。
観光/人口の場合には最大値より上に、5.01や4.43という値がありますが、これらは外れ値といわれます。箱ひげ図の見方や外れ値の考え方は、て、「データの整形と修正」で詳しく解説していますので、よかったら見てください。
以下に簡単ですが、目的のグラフの作成方法を記します。
- 棒グラフ
- データ領域選択
- 「挿入」ー「グラフ」よりグラフの挿入ダイアログを表示
- すべてのグラフタブより、「箱ひげ図」を選択
- タイトル、軸ラベル、データラベルの入力
<RANKING>![]()
高校教育ランキング




コメント